Chapter 19 Entropy and Second Law of Thermodynamics
Learning Objectives:
In this chapter you will basically learn:
\(\bullet\) The second law of thermodynamics: If a process occurs in a closed system, the entropy of the system increases for irreversible processes and remains constant for reversible processes; it never decreases.
\(\bullet\) Identify that entropy is a state function (the value for a particular state of the system does not depend on how that state is reached).
\(\bullet\) Calculate the change in entropy for a process by integrating the inverse of the temperature (in kelvins) with respect to the heat Q transferred during the process.
\(\bullet\) For a phase change with a constant temperature process, apply the relationship between the entropy change \(\Delta S\), the total transferred heat Q, and the temperature T (in kelvins).
\(\bullet\) For an ideal gas, apply the relationship between the entropy change %S and the initial and final values of the pressure and volume.
\(\bullet\) Identify that if a process is an irreversible one, the integration for the entropy change must be done for a reversible process that takes the system between the same initial and final states as the irreversible process.
\(\bullet\) Identify that a heat engine is a device that extracts energy from its environment in the form of heat and does useful work and that in an ideal heat engine, all processes are reversible, with no wasteful energy transfers.
\(\bullet\) Sketch a p-V diagram for the cycle of a Carnot engine, indicating the direction of cycling, the nature of the processes involved, the work done during each process (including algebraic sign), the net work done in the cycle, and the heat transferred during each process (including algebraic sign).
\(\bullet\) Calculate the efficiency \(\varepsilon_c\) of a Carnot engine in terms of the heat transfers and also in terms of the temperatures of the reservoirs.
\(\bullet\) Sketch a p-V diagram for the cycle of a Stirling engine, indicating the direction of cycling, the nature of the processes involved, the work done during each process (including algebraic sign), the net work done in the cycle, and the heat transfers during each process.
\(\bullet\) A refrigerator is a device that uses work to transfer energy from a low-temperature reservoir to a high-temperature reservoir, and that an ideal refrigerator is one that does this with reversible processes and no wasteful losses.
\(\bullet\) Sketch a p-V diagram for the cycle of a Carnot refrigerator, indicating the direction of cycling, the nature of the processes involved, the work done during each process (including algebraic sign), the net work done in the cycle, and the heat transferred during each process (including algebraic sign).
\(\bullet\) Apply the relationship between the coefficient of performance K and the heat exchanges with the reservoirs and the temperatures of the reservoirs.
\(\bullet\) Identify that there is no ideal refrigerator in which all of the energy extracted from the low-temperature reservoir is transferred to the high-temperature reservoir.
\(\bullet\) Identify that the efficiency of a real engine is less than that of the ideal Carnot engine.
\(\bullet\) Apply Boltzmann’s entropy equation to calculate the entropy associated with a multiplicity.
19.1 Entropy
Irreversible Processes and Entropy
Irreversible processes are one-way phenomenon. An irreversible process increases the entropy of the system. Since entropy is a state function, the change in entropy of the system is the same, irrespective of the reversible or irreversible processes. The second law of thermodynamics can be used to determine whether a process is reversible or not.
For example, if you were to catch fire of a match stick, you would be astonished if, later the match stick comes to its original unburned condition. That is obviously the wrong way for the combustion to happen, but the total energy of the closed system would be the same as for the right way.
Thus, changes in energy within a closed system do not set the direction of irreversible processes. Rather, that direction is set by another property that we shall discuss in this chapter—the change in entropy %S of the system.The change in entropy of a system, but we can here state its central property, often called the entropy postulate:
If an irreversible process occurs in a closed system, the entropy S of the system always increases; it never decreases.
Efficiency of any Engine is given by: \[\varepsilon=\frac{energy~we~get}{energy ~we~pay~for}=\frac{|W|}{|Q_H|},~efficiency~ of~ any~ engine\] For a Carnot engine \(W = |Q_H|-|Q_L|.\)Efficiency of a Carnot Engine~ is~ given~ by: \[\varepsilon_C=\frac{|Q_H|-|Q_L|}{|Q_H|}=1-\frac{|Q_L|}{|Q_H|},~efficiency~ of~a~ Carnot~ engine\] Entropy Changes in a Carnot engine, there are two (and only two) reversible energy transfers as heat, and thus two changes in the entropy of the working substance—one at temperature TH and one at TL. The net entropy change per cycle is then
\[\Delta S = \Delta S_H+\Delta S_L=\frac{|Q_H|}{T_H}-\frac{|Q_L|}{T_L}\] Here \(\Delta S_H\) is positive because energy \(|Q_H|\) is added to the working substance as heat (an increase in entropy) and \(\Delta S_L\) is negative because energy \(|Q_L|\) is removed from the working substance as heat (a decrease in entropy). Because entropy is a state function, we must have \(\Delta S = 0\) for a complete cycle. Putting \(\Delta S = 0\), in the above equation we get,
\[\frac{|Q_H|}{T_H}=\frac{|Q_L|}{T_L}\] or
\[\frac{|Q_H|}{T_H}=\frac{|Q_L|}{T_L}\] and the Carnot efficience becomes, \[\varepsilon_C=\frac{|Q_H|-|Q_L|}{|Q_H|}=1-\frac{|T_L|}{|T_H|}=\frac{T_H-T_L}{T_H},~efficiency~ of~a~ Carnot~ engine\] where the temperatures \(T_L\) and \(T_H\) are in kelvins. Because \(T_L < T_H\), the Carnot engine necessarily has a thermal efficiency less than unity—that is, less than 100%.
On the other hand a refrigerator is a device that, operating in a cycle, has workWdone on it as it extracts energy +QL+ as heat from a low-temperature reservoir. The coefficient of performance K of a refrigerator is defined as
\[K=\frac{what~we~want}{what~we~pay~for}=\frac{|Q_L|}{|W|}.\] A Carnot refrigerator is a Carnot engine operating in reverse. Its coefficient of performance is \[K_C=\frac{|Q_L|}{|W|}=\frac{|Q_L|}{|Q_H|-|Q_L|}=\frac{|T_L|}{|T_H|-|T_L|}\]
19.2 ENTROPY IN THE REAL WORLD: ENGINES
19.3 REFRIGERATORS AND REAL ENGINES
19.4 A STATISTICAL VIEW OF ENTROPY
Solved Problems:
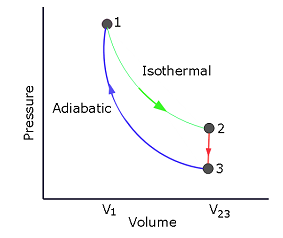
- [17] In Fig. 20-25, where \(V_{23} = 3.00V_1\), n moles of a diatomic ideal gas are taken through the cycle with the molecules rotating but not oscillating. What are (a) \(p_2/p_1\), (b) \(p_3/p_1\), and (c) \(T_3/T_1\)? For path \(1\to 2\), what are (d) \(W/nRT_1\), (e) \(Q/nRT_1\), (f) \(\Delta E_{int}/nRT_1\), and (g) \(\Delta S/nR\)? For path \(2\to 3\), what are (h) \(W/nRT_1\), (i) \(Q/nRT_1\), (j) \(\Delta E_{int}/nRT_1\), (k) \(\Delta S/nR\)? For path \(3\to1\), what are (l) \(W/nRT_1\), (m) \(Q/nRT_1\), (n) \(\Delta E_{int}/nRT_1\), and (o) \(\Delta S/nR\)?
Solution:
For an isothermal process \(T_1=T_2=T\), and for a diatomic ideal gas \(pV=nRT\) \[p_1V_1=nRT\] \[p_2V_2=nRT\] Diving we get, \(\frac{p_2}{p_1}=\frac{V_1}{V_2}=\frac{V_1}{V_{23}}=\frac{V_1}{3.0V_1}=0.33\space(Answer)\)
For an adiabatic process, \(pV^\gamma=constant\), where \(\gamma=\frac{C_P}{C_V}\) is the ratio of molar specific heats for the gas. For diatomic gas \(\gamma=\frac{7}{5}\).
\[p_1V_1^\gamma=constant\] and \[p_3V_3^\gamma=constant\] Dividing we get, \(\frac{p_3}{p_1}=\left(\frac{V_1}{V_3}\right)^{\gamma}=\left(\frac{V_1}{3.0V_1}\right)^{\frac{7}{5}}=0.2148\space(Answer)\)
- We have \(\frac{p_3}{p_1}=\left(\frac{V_1}{V_3}\right)^{\gamma}\)
Also, \[p_1V_1=nRT_1\]
and \[p_3V_3=nRT_3\]
Dividing, we get \[\frac{T_3}{T_1}=\left(\frac{p_3}{p_1}\right)\left(\frac{V_3}{V_1}\right)=\left(\frac{V_1}{V_3}\right)^{\gamma-1}=\left(\frac{V_1}{3.0V_1}\right)^{\gamma-1}=\left(\frac{V_1}{3.0V_1}\right)^{(7/5)-1}=0.6444\space(Answer)\]
- For an ideal gas and an isothermal process, work done can be expressed as \[W=nRT\ln\frac{V_f}{V_i}=\]
\[\frac{W}{nRT_1}=\ln\frac{V_2}{V_1}=\ln\frac{3.0V_1}{V_1}=1.0986\space(Answer)\] (e) Using First Law of Thermodynamics \(W=Q-E_{int}\). Since, \(E_{int}=0, W = Q\), hence \[\frac{W}{nRT_1}=\frac{Q}{nRT_1}=\ln\frac{V_2}{V_1}=\ln\frac{3.0V_1}{V_1}=1.0986\space(Answer)\] (f) Using Using First Law of Thermodynamics \(W=Q-E_{int}\). Since, \(E_{int}=0\) \[\frac{E_{int}}{nRT_1}= 0\] (g) We know entropy is related to \(\Delta S=\frac{Q}{T}\) and we know Using Using First Law of Thermodynamics \(W=Q-E_{int}\). Since, \(E_{int}=0\) \[W=Q\] Also, using \[\frac{W}{nRT_1}=\ln\frac{V_2}{V_1}\]
\[Q=nRT_1\ln\frac{V_2}{V_1}=nRT_1\ln\frac{3.0V_1}{V_1}=(1.099)nRT_1\] Therefore, \[\Delta S=\frac{Q}{T_1}=\frac{(1.099)nRT_1}{T_1}\], and \[\frac{\Delta S}{nR}=1.099\space(Answer)\] (h) Work done can be calculated to be \(W=p\Delta V=p(V_2-V_3)=0\), since \(V_2=V_3\) Therefore, \[\frac{W}{nRT_1}=0\] (i) Using First Law of Thermodynamics, \(W=Q-E_{int}\). Since, \(W=0\), \(Q=E_{int}\) \[\frac{Q}{nRT_1}=\frac{E_{int}}{nRT_1}=\frac{nC_v\Delta T}{nRT_1}=\frac{nC_v(T_3-T_2)}{nRT_1}\] Substitute \(T_2 = T_1\), \(C_v=\frac{5}{2}R\) and \(\frac{T_3}{T_1}=\left(\frac{V_1}{V_3}\right)^{\gamma-1}\) in the above equation, we get \[\frac{E_{int}}{nRT_1}=\frac{nC_v(T_3-T_2)}{nRT_1}=\frac{n(5/2)RT_1((V_1/V_3)^{\gamma-1}-1)}{nRT_1}\] \[=(5/2)((1/3)^{(7/5)-1}-1)=-0.889\space(Answer)\] (j) Since work done is zero for path 2 to 3, then from first law of thermodynamics we get \[0=Q-E_{int}\] Therefore, we get \[\frac{Q}{nRT_1}=\frac{nC_v(T_3-T_2)}{nRT_1}=\frac{n(5/2)RT_1((V_1/V_3)^{\gamma-1}-1)}{nRT_1}\] \[=(5/2)((1/3)^{(7/5)-1}-1)=-0.889\space(Answer)\] (k) Change in entropy for the path can be found using \[\Delta S=S_f-S_i=nR\ln\frac{V_3}{V_2}+nC_v\ln\frac{T_3}{T_2}\] Since \(V_3=V_2\), the first term of the above equation will drop out, \(T_2=T_1\), we get
\[\Delta S=nC_v\ln\frac{T_3}{T_2}\] \[\frac{\Delta S}{nR}=\frac{5}{2}\ln\frac{T_3}{T_2}=\frac{\frac{5}{2}\ln T_1\left(\frac{V_1}{V_3}\right)^{\gamma-1}}{T_1}=\frac{5}{2}\ln \left(\frac{V_1}{3V_1}\right)^{7/2-1}=-1.0986\space(Answer)\] where we made use of \(T_2=T_1\) and \(T_3=\ln \left(\frac{V_1}{3V_1}\right)^{7/2-1}\)’
- Using First Law of Thermodynamics, \(W=Q-E_{int}\). Since, \(Q=0\), \(W=-E_{int}\) \[\frac{W}{nRT_1}=-\frac{E_{int}}{nRT_1}=-\frac{nC_v\Delta T}{nRT_1}=\frac{nC_v(T_3-T_1)}{nRT_1}\] Substitute \(C_v=\frac{5}{2}R\) and \(\frac{T_3}{T_1}=\left(\frac{V_1}{V_3}\right)^{\gamma-1}\) in the above equation, we get \[\frac{W}{nRT_1}=-\frac{nC_v(T_3-T_2)}{nRT_1}=-\frac{n(5/2)RT_1((V_1/V_3)^{\gamma-1}-1)}{nRT_1}\] \[=-(5/2)((1/3)^{(7/5)-1}-1)=0.889\space(Answer)\]
- Since, Q=0, \(\frac{Q}{nRT_1}=0\)
- Also, since \(W=-E_{int}\),
\[\frac{E_{int}}{nRT_1}=\frac{nC_v(T_3-T_2)}{nRT_1}=\frac{n(5/2)RT_1((V_1/V_3)^{\gamma-1}-1)}{nRT_1}=(5/2)((1/3)^{(7/5)-1}-1)=-0.889\space(Answer)\] (o) Since Q - 0, Therefore, \[\Delta S=\frac{Q}{T_1}=0\] Also, \[\frac{\Delta S}{nR}=0\space(Answer)\]
- [19] Suppose 1.00 mol of a monatomic ideal gas is taken from initial pressure \(p_1\) and volume \(V_1\) through two steps: (1) an isothermal expansion to volume \(2.00V_1\) and (2) a pressure increase to \(2.00p_1\) at constant volume. What is \(Q/p_1V_1\) for (a) step 1 and (b) step 2? What is \(W/p_1V_1\) for (c) step 1 and (d) step 2? For the full process, what are (e) \(\Delta E_{int}/p_1V_1\) and (f) \(\Delta S\)? The gas is returned to its initial state and again taken to the same final state but now through these two steps: (1) an isothermal compression to pressure \(2.00p_1\) and (2) a volume increase to \(2.00V_1\) at constant pressure. What is \(Q/p_1V_1\) for (g) step 1 and (h) step 2? What is \(W/p_1V_1\) for (i) step 1 and (j) step 2? For the full process, what are (k) \(\Delta E_{int}/p_1V_1\) and (l) \(\Delta S\)?
Solution: (a) Using First Law of Thermodynamics (see Table 18-5), \(\Delta E_{int}=Q-W\), and for an isothermal to volume from initial volume of \(V_1\) to \(2.00V_1\),\(E_{int}=0\), we get \[Q=W=nRTln\frac{V_2}{V_1}=p_1V_1ln\frac{2V_1}{V_1}\] \[\frac{Q}{p_1V_1}=ln\frac{2V_1}{V_1}=0.693\space(Answer)\] (b) Using First Law of Thermodynamics (see Table 18-5), \(\Delta E_{int}=Q-W\), and for a pressure increase to \(2.00p_1\) at constant volume, W = 0, we get \[E_{int}=Q=nC_v\Delta T=nC_v(T_2-T_1)=n\frac{f}{2}R\left(\frac{p_2V_2}{nR}-\frac{p_1V_1}{nR}\right)\] \[Q=n\frac{3}{2}R\left(\frac{2p_12V_1}{nR}-\frac{p_1V_1}{nR}\right) =\frac{9}{2}p_1V_1\] where we made use of f =3 for monoatomic gas. \[\frac{Q}{p_1V_1}=\frac{9}{2}=4.5\space(Answer)\] (c) We make use of the result of (a), where \[Q=W=nRTln\frac{V_2}{V_1}=p_1V_1ln\frac{2V_1}{V_1}\] Therefore, \[\frac{W}{p_1V_1}=ln\frac{2V_1}{V_1}=0.693\space(Answer)\] (d) The work done for constant volume, W =0. Therefore,\[\frac{W}{p_1V_1}=ln\frac{V_1}{V_1}=0.0\space(Answer)\] (e) We have in part (a) \(\Delta E_{int} = 0\), (b) \(\frac{\Delta E_{int}}{p_1V_1} =\frac{9}{2}\), and in (c) again \(\Delta E_{int} = 0\). Therefore,
\(\frac{\Delta E_{int}}{p_1V_1} =\frac{9}{2}\space(Answer)\) (f) \[\Delta S = nR\ln\frac{V_2}{V_1}+C_v\ln\frac{T_2}{T_1}=nR\ln\frac{2V_1}{V_1}+\frac{5}{2}R\ln\frac{4T_1}{T_1}\] \[\Delta S = nR\ln\frac{2V_1}{V_1}+\frac{3}{2}R\ln\frac{4T_1}{T_1}=(1~mol)(8.31~J/mol.K)\ln(2)+\frac{3}{2}(8.31~J/mol.K)\ln(4)\] \[\Delta S=23.04\space\frac{J}{K}\space(Answer)\] (g) Using First law of thermodynamics, and for an isothermal compression to \(2p_1\) \(E_{int}=0\). Therefore, \[Q=W=p_1V_1\ln\frac{V_2}{V_1}\] \[\frac{Q}{p_1V_1}=\ln\frac{V_2}{V_1}=\ln\frac{V_1}{2V_1}=-0.693\space(Answer)\]
- A volume increase to \(2.00V_1\) at constant pressure. \[Q=nC_p\Delta T= nC_p(T_2-T_1)= n(C_v+R)(T_2-T_1)=n(\frac{3}{2}R+R)(T_2-T_1)\] \[Q = n(\frac{5}{2}R)(T_2-T_1)=\frac{5}{2}nR\left(\frac{4p_1V_1}{nR}-\frac{p_1V_1}{nR}\right)=\frac{15}{2}p_1V_1=7.50p_1V_1\space\] \[\frac{Q}{p_1V_1}=7.50\space(Answer)\]
- For an isothermal compression, work done will be same as (g) that is, \(2p_1\) \(E_{int}=0\). Therefore, \[W=Q=p_1V_1\ln\frac{V_2}{V_1}\] \[\frac{W}{p_1V_1}=\ln\frac{V_2}{V_1}=\ln\frac{V_1}{2V_1}=-0.693\space(Answer)\]
- Work done \[W=p\Delta V= p(V_2-V_1)=2p_1(2V_1-\frac{1}{2}V_1=3p_1V_1\] \[\frac{W}{p_1V_1}=3.00\space(Answer)\]
- Using First Law of Thermodynamics \(E_{int}= Q-W\), we can calculate the internal energy for the full process using the results that we got in the previous parts as follows:
\[E_{int}= Q-W= -0.693p_1V_1+7.50p_1V_1+0.693p_1V_1-3.00p_1V_1=4.50p_1V_1\] \[\frac{E_{int}}{p_1V_1}=4.50\space(Answer)\] (l) The change in entropy for the full process \[\Delta S = nR\ln\frac{V_2}{V_1}+C_v\ln\frac{T_2}{T_1}=nR\ln\frac{2V_1}{V_1}+\frac{5}{2}R\ln\frac{4T_1}{T_1}\] \[\Delta S = nR\ln\frac{2V_1}{V_1}+\frac{3}{2}R\ln\frac{4T_1}{T_1}=(1~mol)(8.31~J/mol.K)\ln(2)+\frac{3}{2}(8.31~J/mol.K)\ln(4)\] \[\Delta S=23.04\space\frac{J}{K}\space(Answer)\]
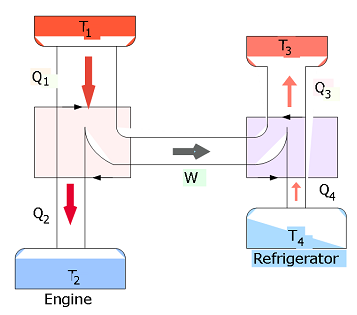
- [43] Figure 20-32 represents a Carnot engine that works between temperatures \(T_1 = 400\) K and \(T_2 = 150\) K and drives a Carnot refrigerator that works between temperatures \(T_3 = 325\) K and \(T_4 = 225\) K. What is the ratio \(Q_3/Q_1\)?
Solution: Efficiency of any Engine is given by: \[\varepsilon=\frac{energy~we~get}{energy ~we~pay~for}=\frac{|W|}{|Q_H|},~efficiency~ of~ any~ engine\] For a Carnot engine \(W = |Q_H|-|Q_L|.\)Efficiency of a Carnot Engine~ is~ given~ by: \[\varepsilon_C=\frac{|Q_H|-|Q_L|}{|Q_H|}=1-\frac{|Q_L|}{|Q_H|},~efficiency~ of~a~ Carnot~ engine\] Entropy Changes in a Carnot engine, there are two (and only two) reversible energy transfers as heat, and thus two changes in the entropy of the working substance—one at temperature TH and one at TL. The net entropy change per cycle is then
\[\Delta S = \Delta S_H+\Delta S_L=\frac{|Q_H|}{T_H}-\frac{|Q_L|}{T_L}\] Here \(\Delta S_H\) is positive because energy \(|Q_H|\) is added to the working substance as heat (an increase in entropy) and \(\Delta S_L\) is negative because energy \(|Q_L|\) is removed from the working substance as heat (a decrease in entropy). Because entropy is a state function, we must have \(\Delta S = 0\) for a complete cycle. Putting \(\Delta S = 0\), in the above equation we get,
\[\frac{|Q_H|}{T_H}=\frac{|Q_L|}{T_L}\] or
\[\frac{|Q_H|}{T_H}=\frac{|Q_L|}{T_L}\] and the Carnot efficience becomes, \[\varepsilon_C=\frac{|Q_H|-|Q_L|}{|Q_H|}=1-\frac{|T_L|}{|T_H|}=\frac{T_H-T_L}{T_H},~efficiency~ of~a~ Carnot~ engine\] where the temperatures \(T_L\) and \(T_H\) are in kelvins. Because \(T_L < T_H\), the Carnot engine necessarily has a thermal efficiency less than unity—that is, less than 100%.
On the other hand a refrigerator is a device that, operating in a cycle, has workWdone on it as it extracts energy +QL+ as heat from a low-temperature reservoir. The coefficient of performance K of a refrigerator is defined as
\[K=\frac{what~we~want}{what~we~pay~for}=\frac{|Q_L|}{|W|}.\] A Carnot refrigerator is a Carnot engine operating in reverse. Its coefficient of performance is \[K_C=\frac{|Q_L|}{|W|}=\frac{|Q_L|}{|Q_H|-|Q_L|}=\frac{|T_L|}{|T_H|-|T_L|}\] In our given problem, for Carnot engine, \(T_H=T_1=400~K\) and \(T_L=T_2=150~K\), and for Carnot refrigerator, \(T_H=T_3=325~K\) and \(T_L=T_4=225~K\). The work done by the Carnot engine is same as the work done by the refrigerator, and substituting \(Q_4=Q_3-W\) and equating we get
\[\frac{|Q_3|}{|Q_1|}=\frac{1-\frac{|T_2|}{|T_1|}}{1-\frac{|T_4|}{|T_3|}}=\frac{1-\frac{|150|}{|400|}}{1-\frac{|225|}{|325|}}=2.03~(Answer)\]
- [46] A box contains N identical gas molecules equally divided between its two halves. For N = 50, what are (a) the multiplicity W of the central configuration, (b) the total number of microstates, and (c) the percentage of the time the system spends in the central configuration? For N = 100, what are (d) W of the central configuration, (e) the total number of microstates, and (f) the percentage of the time the system spends in the central configuration? For N = 200, what are (g) W of the central configuration, (h) the total number of microstates, and (i) the percentage of the time the system spends in the central configuration? (j) Does the time spent in the central configuration increase or decrease with an increase in N?
Solution:
Given N = 50, multiplicity W of the central configuration, \[W=\frac{N!}{n_1!n_2!}=\frac{50!}{25!25!}=1.264\times 10^{14}~(Answer)\]
Given N = 50, the total number of microstates, \[N_{total}=2^N=2^{50}=1.126\times 10^{15}~(Answer)\]
Percent of the time the system spends in the central configuration can be found by \[\frac{W}{N_{total}}=\frac{1.264\times 10^{14}}{1.126\times 10^{15}}\times 100=11.226\%~(Answer)\]
Given N = 100, multiplicity W of the central configuration, \[W=\frac{N!}{n_1!n_2!}=\frac{100!}{50!50!}=1.0\times 10^{29}~(Answer)\]
Given N = 100, the total number of microstates, \[N_{total}=2^N=2^{100}=1.268\times 10^{30}~(Answer)\]
Percent of the time the system spends in the central configuration can be found by \[\frac{W}{N_{total}}=\frac{1.0\times 10^{29}}{1.268\times 10^{30}}\times 100=7.886\%~(Answer)\]
Given N = 200, multiplicity W of the central configuration, \[W=\frac{N!}{n_1!n_2!}=\frac{200!}{100!100!}=9.3\times 10^{58}~(Answer)\]
Given N = 200, the total number of microstates, \[N_{total}=2^N=2^{200}=1.607\times 10^{60}~(Answer)\]
Percent of the time the system spends in the central configuration can be found by \[\frac{W}{N_{total}}=\frac{9.3\times 10^{58}}{1.607\times 10^{60}}\times 100=5.787\%~(Answer)\]
Time spent in the central configuration decreases with an increase in N. (Answer)
Problems:
Section 19-1 Entropy
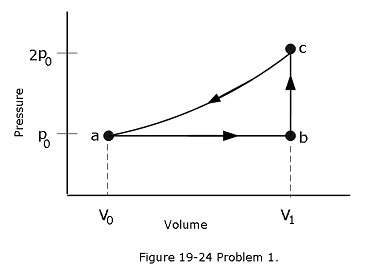
- [14] (a) For 1.0 mol of a monatomic ideal gas taken through the cycle in Fig. 19-24, where \(V_1 = 4.00V_0\), what is \(W/p_0V_0\) as the gas goes from state a to state c along path abc? What is \(\Delta E_{int}/p_0V_0\) in going (b) from b to c and (c) through one full cycle? What is \(\Delta S\) in going (d) from b to c and (e) through one full cycle?
- [20] Expand 1.00 mol of an monatomic gas initially at 5.00 kPa and 600 K from initial volume \(V_i = 1.00 m^3\) to final volume \(V_f = 2.00 m^3\).At any instant during the expansion, the pressure p and volume V of the gas are related by \(p = 5.00 exp[(V_i - V)/a]\), with p in kilopascals, \(V_i\) and V in cubic meters, and \(a = 1.00 m^3\).What are the final (a) pressure and (b) temperature of the gas? (c) How much work is done by the gas during the expansion? (d) What is \(\Delta S\) for the expansion? (Hint: Use two simple reversible processes to find \(\Delta S\).)
Section 19-2 Entropy in the Real World: Engines
[26] In a hypothetical nuclear fusion reactor, the fuel is deuterium gas at a temperature of \(7 \times 10^8\) K. If this gas could be used to operate a Carnot engine with \(T_L = 100^\circ\) C, what would be the engine’s efficiency? Take both temperatures to be exact and report your answer to seven significant figures.
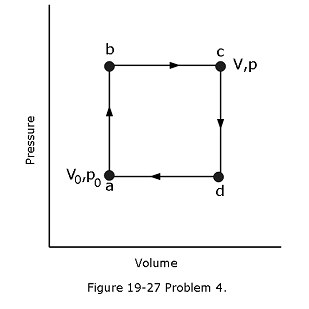
[29] Figure 19-27 shows a reversible cycle through which 1.00 mol of a monatomic ideal gas is taken. Assume that \(p = 2p_0\), \(V = 2V_0\), \(p_0 = 1.01 \times 10^5\) Pa, and \(V_0 = 0.0225 m^3\). Calculate (a) the work done during the cycle, (b) the energy added as heat during stroke abc, and (c) the efficiency of the cycle. (d) What is the efficiency of a Carnot engine operating between the highest and lowest temperatures that occur in the cycle? (e) Is this greater than or less than the efficiency calculated in (c)?
[31] The efficiency of a particular car engine is 25% when the engine does 8.2 kJ of work per cycle. Assume the process is reversible. What are (a) the energy the engine gains per cycle as heat \(Q_{gain}\) from the fuel combustion and (b) the energy the engine loses per cycle as heat \(Q_{lost}\)? If a tune-up increases the efficiency to 31%, what are (c) \(Q_{gain}\) and (d) \(Q_{lost}\) at the same work value?
In a coal-fired utility boiler, the temperature of high pressure steam \(T_H\) is about 540°C and \(T_L\), the cooling tower water temperature, is about 27°C. Calculate the Carnot efficiency of the power plant.
Solution:
Carnot efficiency depends on high temperature and low temperatures between which the heat engine operates. We are given both temperatures. However, the temperatures need to be converted to Kelvin:
\[T_H=540^\circ C+273=813K\] \[T_L=27oC+273=300 ~K\] \[\varepsilon_C=\frac{|Q_H|-|Q_L|}{|Q_H|}=1-\frac{|T_L|}{|T_H|}=\frac{T_H-T_L}{T_H},~efficiency~ of~a~ Carnot~ engine\]
\[\varepsilon_C=1-\frac{|T_L|}{|T_H|}=\frac{T_H-T_L}{T_H}=\frac{813-300}{813}\times 100 = 63\%\space (Answer\]
From the Carnot Efficiency formula, it can be inferred that a maximum of 63.10% of the fuel energy can go to generation. To make the Carnot efficiency as high as possible, either Thot should be increased or Tcold (temperature of heat rejection) should be decreased.
- If an automobile engine burns gasoline at a temperature of \(T_H=1089~K\) and the ambient temperature is \(T_L = 294~K\), what is its maximum possible efficiency.
\[\varepsilon_C=\frac{|Q_H|-|Q_L|}{|Q_H|}=1-\frac{|T_L|}{|T_H|}=\frac{T_H-T_L}{T_H},~efficiency~ of~a~ Carnot~ engine\]
\[\varepsilon_C=1-\frac{|T_L|}{|T_H|}=\frac{T_H-T_L}{T_H}=\frac{1089-294}{1089}\times 100 = 73\%\space (Answer\] Note that the Carnot efficiency formula is an idealized mathematical models of engines, with no friction and working fluids that obey simple thermodynamic rules called the ideal gas law. Real engines have many departures from ideal behavior that waste energy, reducing actual efficiencies much lower than the theoretical that we calculated above.
Section 19-3 Refrigerators and Real Engines
[40] To make ice, a freezer that is a reverse Carnot engine extracts 42 kJ as heat at \(-15^\circ\) C during each cycle, with coefficient of performance 5.7. The room temperature is \(30.3^\circ\) C. How much (a) energy per cycle is delivered as heat to the room and (b) work per cycle is required to run the freezer?
[44] (a) During each cycle, a Carnot engine absorbs 750 J as heat from a high-temperature reservoir at 360 K, with the low-temperature reservoir at 280 K. How much work is done per cycle? (b) The engine is then made to work in reverse to function as a Carnot refrigerator between those same two reservoirs. During each cycle, how much work is required to remove 1200 J as heat from the low-temperature reservoir?
Section 19-4 A Statistical View of Entropy
- [47] A box contains N gas molecules. Consider the box to be divided into three equal parts. (a) By extension of Eq. 20-20, write a formula for the multiplicity of any given configuration. (b) Consider two configurations: configuration A with equal numbers of molecules in all three thirds of the box, and configuration B with equal numbers of molecules in each half of the box divided into two equal parts rather than three. What is the ratio \(W_A/W_B\) of the multiplicity of configuration A to that of configuration B? (c) Evaluate \(W_A/W_B\) for N = 100. (Because 100 is not evenly divisible by 3, put 34 molecules into one of the three box parts of configuration A and 33 in each of the other two parts.)