Chapter 3 Vectors & Scalars

Learning Objectives:

In this chapter you will basically learn:

$\bullet$ Learn how you define a vector, vector addition, vector subtraction, commutative and associative laws of vectors.

$\bullet$ Learn what are orthogonal coordinate systems; cartesian, cylindrical and spherical coordinates. Learn how to calculate the components of a vector in cartesian and polar coordinate system and determine its magnitude and direction.

$\bullet$ Learn how to represent a vector in terms of unitvector notations and apply in addition and subtraction of vectors.

$\bullet$ Learn how to multiply vectors by scalars, dot (or scalar) product of two vectors, gives a scalar, the cross (or vector) product gives a new vector that is perpendicular to the plane of original two. Product of three vectors.

$\bullet$ Learn the right-hand rule to find the direction of the vector that results from a cross product.

$\bullet$ Gradient of a scalar field, divergence of a vector field, Divergence theorem, Stoke’s theorem, and curl of a vector.

3.1 Fundamental Quantities:

In mechanics we use the fundamental quantities that include two scalars,

$\bullet$ mass m and

$\bullet$ time t ,

and the two vectors,

$\bullet$ position vector $\vec r$, and

$\bullet$ force vector $\vec F$ (acting on a system of interest).

Scalars are represented with unbolded font (t and m) and vectors are typed with an arrow on top ($\vec r$, $\vec F$).

We are familiar with how scalar arithmetic and algebra of addition, subtraction, multiplication and division can be performed with ordinary numbers and their corresponding symbols. In dealing with Newtonian mechanics we will require the vector arithmetic and that will be explained with examples in this chapter.

3.2 Defining Vectors:

A scalar (possibly dimensional) is just a single number with magnitude and a sign, whereas a vector (possibly dimensional) is a quantity that is fully described by both magnitude and its associated direction.

Vectors follow certain (vector) rules of addition, subtraction, multiplication and perhaps division. Vector quantities such as displacement, velocity, acceleration have both magnitude and direction and thus can be represented with vectors.

One can argue that $\vec F$ is not a fundamental quantity because it is the product of scalar m and and a vector $\vec a$ which is, in turn defined in terms of $\vec r$ and t. But in the Engineering convention both $\vec F$ and $\vec a$ are treated to be vector quanties.

Some physical quantities such as temperature, pressure, energy, mass, and time, do not “point” in the spatial sense. We call such quantities scalars, and we deal with them by the rules of ordinary algebra. A single value, with a sign (as in a temperature of -40°F), specifies a scalar.

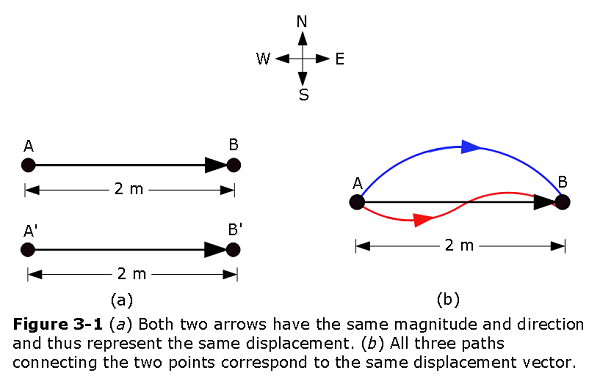
If a particle changes its position Eastward with a magnitude of 2 m moving from A to B in Fig. 3-1a, we say that it undergoes a displacement from A to B, which we represent with an arrow pointing from A to B. The arrow specifies the vector graphically. In Fig. 3-1a, the arrows from A to B, and from A’ to B’have the same magnitude and direction. Thus, they specify identical displacement vectors and represent the same change of position for the particle.

The displacement vector tells us nothing about the actual path that the particle takes. In Fig. 3-1b, for example, all three paths connecting points A and B correspond to the same displacement vector, that of Fig. 3-1a. Displacement vectors represent only the overall effect of the motion, not the motion itself.

3.3 Adding Vectors Geometrically

The sum of two vectors $\vec a$ and $\vec b$ is defined by the tip to tail rule of vector addition shown in Fig. 3.2a for the sum $\vec s = \vec a + \vec b$. Vector $\vec a$ is drawn and then vector $\vec b$ is drawn with its tail at the tip (or head) of $\vec a$. The sum $\vec s$ is the vector from the tail of $\vec a$ to the tip of $\vec b$.

In Fig. 3-2b, the same sum is achieved if $\vec b$ is drawn first, and then and then vector $\vec a$ is drawn with its tail at the tip (or head) of $\vec b$. The sum $\vec s$ is the vector from the tail of $\vec b$ to the tip of $\vec a$.

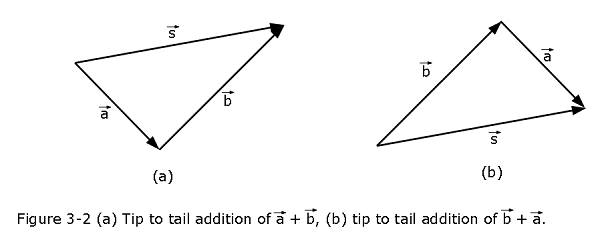
A symbol with an overhead arrow always implies both properties of a vector, magnitude and direction. We can represent the relation among the three vectors in Fig. 3-2 with the vector equation

\[\begin{equation} \vec s = \vec a + \vec b \tag{3.1} \end{equation}\]

3.4 Commutative and Associative Laws of Vector Addition

Putting both ways of adding $\vec a$ and $\vec b$ on the same picture draws a parallelogram as shown in Fig. 3.3. Hence the tip to tail rule of vector addition is also called the parallelogram rule. The parallelogram construction shows the commutative property of vector addition, namely that $\vec a + \vec b = \vec b + \vec a$.

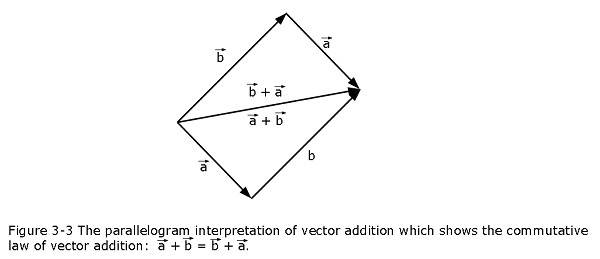
\[\begin{equation} \vec a + \vec b = \vec b + \vec a \space (commutative \space law) \tag{3.2} \end{equation}\]

In case of adding more than two vectors, we can group them in any order as we add them. Thus, if we want to add vectors $\vec a$, $\vec b$, and $\vec c$, we can add $\vec a$ and $\vec b$ first and then add their vector sum to $\vec c$. We can also add $\vec b$ and $\vec c$ first and then add that sum to $\vec a$. We get the same result either way, as shown in Fig. 3-4.That is,

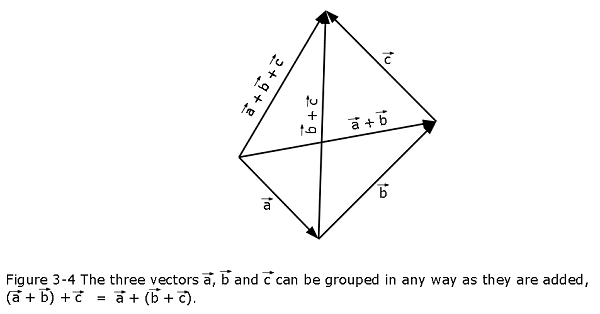
\[\begin{equation} (\vec a + \vec b) + \vec c = \vec a + (\vec b + \vec c) \space (associative \space law) \tag{3.3} \end{equation}\]

3.5 Subtraction, Negation, and the Zero Vector

Subtraction is most simply defined by inverse addition. Find $\vec c - \vec a$ means find the vector which when added to $a $ gives $\vec c$. We can draw $\vec c$, draw $\vec a$ and then find the vector which, when added tip to tail to $\vec a$ give $\vec c$. Figure 3.2a shows that B answers the question. Another interpretation comes from defining the negative of a vector

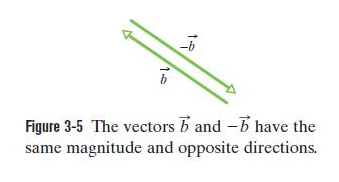
In case of vector subtraction, the vector $-\vec b$ is a vector with the same magnitude as $\vec b$ but the opposite direction (see Fig. 3-5).Adding the two vectors in Fig. 3-5 would yield

$\vec b + (-\vec b) = 0$

Thus, adding $-\vec b$ has the effect of subtracting $\vec b$. We use this property to define the difference between two vectors: let $\vec d = \vec a - \vec b$ as can be seen in Fig. 3-6.

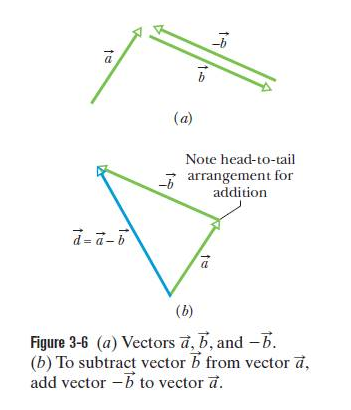
Then

\[\begin{equation} \vec d = \vec a - \vec b = \vec a + (-\vec b) \space (vector \space subtraction) \tag{3.4} \end{equation}\]

3.6 Components of Vectors

Any vector can be resolved into its components. A component of a vector is the projection of the vector along the axes. In Fig. 3-7, $a_x$ is the component of vector $\vec a$ on the x axis and $a_y$ is the component along the y axis. To find the projection of a vector along an axis, we draw perpendicular lines from the two ends of the vector to the axis.The projection of a vector on an x axis is its x component, and similarly the projection on the y axis is the y component. The process of finding the components of a vector is called resolving the vector.

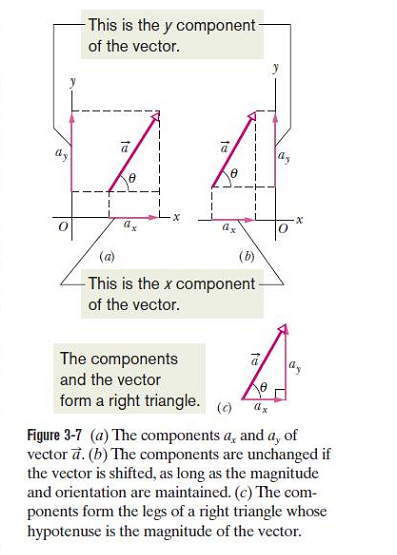
The components of $\vec a$ in Fig. 3-7a can be found geometrically from the right triangle:

\[\begin{equation} a_x = a~cos\theta \space\space\space and \space\space\space a_y = a~sin\theta \tag{3.5} \end{equation}\]

We can find the magnitude of the vector $\vec a$ and its direction using the following equations:

\[\begin{equation} a = \sqrt{a_{x}^2 + a_{y}^2} \space\space\space and \space\space\space tan\theta = \frac{a_y}{a_x} \tag{3.6} \end{equation}\]

3.7 Unit Vectors, adding Vectors by Components

A unit vector is a vector that has a magnitude of exactly 1 and points in a particular direction. The unit vectors in the positive directions of the x, y, and z axes are labeled $\hat i$, $\hat j$, and $\hat k$, where the hat is used to represent unit vector as shown in Fig. 3-7.The arrangement of axes in Fig. 3-7 is said to be a right-handed coordinate system.

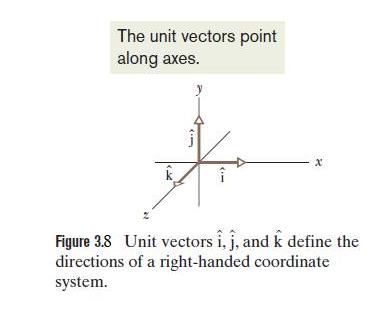
In terms of unit vectors, vectors $\vec a$ and $\vec b$ can be represented as follows:

\[\begin{equation} \vec a = \hat i a_x + \hat j a_y + \hat k a_z \tag{3.7} \end{equation}\]

\[\begin{equation} \vec b = \hat i b_x + \hat j b_y + \hat k b_z \tag{3.8} \end{equation}\]

Now if we add $\vec a$ and $\vec b$ the components of the resultant vector \[\begin{equation} \vec r = \hat i r_x + \hat j r_y + \hat k r_z = \vec a + \vec b = \hat i (a_x + b_x) + \hat j (a_y + b_y) + \hat k (a_z + b_z) \tag{3.9} \end{equation}\]

where the components of vector $\vec r$ are as follows: \[\begin{equation} r_x = (a_x + b_x) \tag{3.10} \end{equation}\]

\[\begin{equation} r_y = (a_y + b_y) \tag{3.11} \end{equation}\]

\[\begin{equation} r_z = (a_z + b_z) \tag{3.12} \end{equation}\]

Similarly, if we subtract $\vec a$ and $\vec b$ the components of the resultant vector

\[\begin{equation} \vec d = \hat i d_x + \hat j d_y + \hat k d_z = \vec a - \vec b = \hat i (a_x - b_x) + \hat j (a_y - b_y) + \hat k (a_z - b_z) \tag{3.13} \end{equation}\]

where the components of vector $\vec d$ are as follows: \[\begin{equation} d_x = (a_x - b_x) \tag{3.14} \end{equation}\]

\[\begin{equation} d_y = (a_y - b_y) \tag{3.15} \end{equation}\]

\[\begin{equation} d_z = (a_z - b_z) \tag{3.16} \end{equation}\]

3.7.1 Multiplying a Vector by a Scalar

The multiplication of a vector by a scalar s, we get a new vector. The new vector has the magnitude is the product of the magnitude of $\vec a$ and the absolute value of s. Its direction is the direction of $\vec a$ if s is positive but the opposite direction if s is negative. Similar to multiplication we can also divide vector $\vec a$ by s, by simply multiplying $\vec a$ by 1/s.

3.7.2 Multiplying a Vector by a Vector

There are two types of vector multiplication. One type of vector multiplication produces a scalar (commonly known as the dot or scalar product), and the other type of multiplication produces a new vector (commonly known as the cross or vector product).

The Dot or Scalar Product

The dot or scalar product of the vectors $\vec a$ and $\vec b$ in Fig. 3-8a is written as $\vec a.\vec b$ and defined to be

\[\begin{equation} \vec a.\vec b = ab~\cos\phi \tag{3.17} \end{equation}\]

where a is the magnitude of $\vec a$, b is the magnitude of $\vec b$, and $\phi$ is the angle between $\vec a$ and $\vec b$.The angle between $\vec a$ and $\vec b$ could be either $\phi$ or ($360^o-\phi$). Either of these angles can be used in Eq. 3-17, because their cosines lead to the same results.

Equation 3-17 can be written in two different formats as follows:

\[\begin{equation} \vec a.\vec b = (a~cos\phi)b = a(b~cos\phi) \tag{3.18} \end{equation}\]

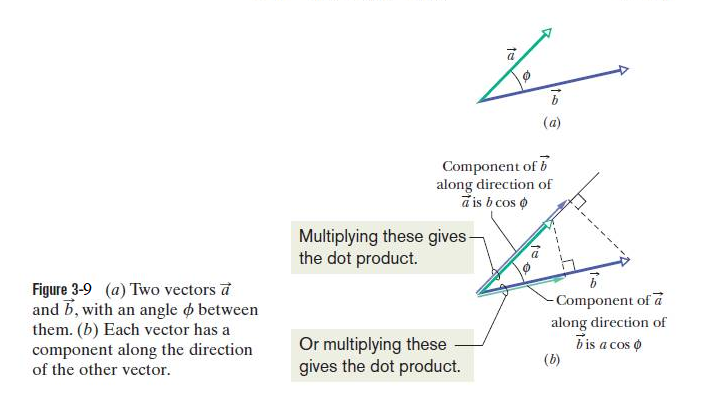
The results of multiplying two vectors using dot or scalar product follow the commutative law, so we can write

\[\begin{equation} \vec a.\vec b = \vec b.\vec a \tag{3.19} \end{equation}\]

\[\begin{equation} \vec a.\vec b = (\hat i a_x + \hat j a_y + \hat k a_z).(\hat i b_x + \hat j b_y + \hat k b_z )=a_x.b_x + a_y.b_y + a_z.b_z \tag{3.20} \end{equation}\]

\[\begin{equation} \vec b.\vec a = (\hat i b_x + \hat j b_y + \hat k b_z ).(\hat i a_x + \hat j a_y + \hat k a_z) = b_x.a_x + b_y.a_y + b_z.a_z \tag{3.21} \end{equation}\]

The Cross or Vector Product

The vector or cross product of $\vec a$ and $\vec b$, written as $\vec a \times \vec b$, creates a third vector$\vec c$ whose magnitude is

\[\begin{equation} c = ab~sin\phi \tag{3.22} \end{equation}\]

The direction of $\vec c$ is perpendicular to the plane that contains $\vec a$ and $\vec b$. Where $\phi$ is the smaller of the two angles between $\vec a$ and $\vec b$. One must use smaller of the two angles between the vectors because $sin \phi$ and $sin (360^0-\phi)$ differ in algebraic sign. If $\vec a$ and $\vec b$ are parallel or antiparallel, $\vec a \times \vec b = 0$.The magnitude of $\vec a \times \vec b$ which can be written as $|\vec a \times \vec b|$, is maximum when and are perpendicular to each other.

The direction of $\vec c$ is perpendicular to the plane that contains $\vec a$ and $\vec b$. Figure 3-9a shows how to determine the direction of $\vec c = \vec a \times \vec b$ with what is known as a right-hand rule.

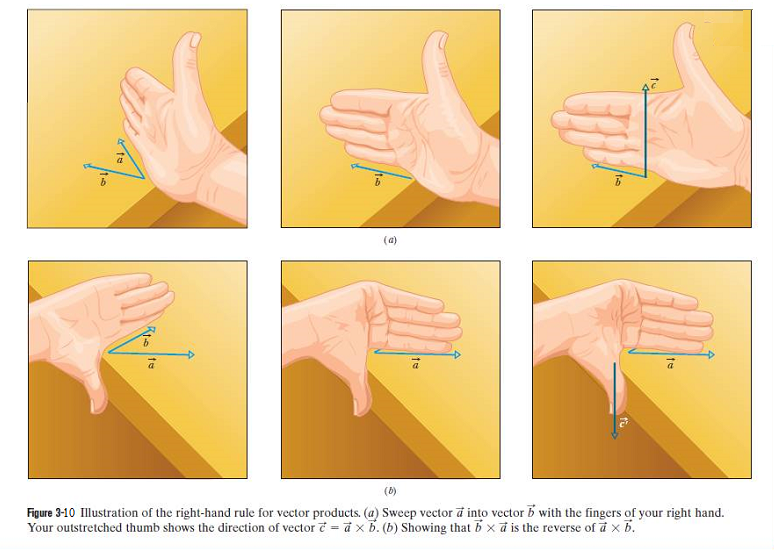
The order of the vector multiplication is important. In Fig. 3-9b, the direction of $\vec c' = \vec b \times \vec a$, is in the opposite direction of $\vec c$, that is $\vec c' = -\vec c$ as given in the following equation.

\[\begin{equation} \vec b \times \vec a = -(\vec a \times \vec b) \tag{3.23} \end{equation}\]

In unit vector notation the cross product of $\vec a \times \vec b$ is

\[\begin{equation} \vec a \times \vec b = (\hat i a_x + \hat j a_y + \hat k a_z) \times (\hat i b_x + \hat j b_y + \hat k b_z) \tag{3.24} \end{equation}\]

Vector multiplication can be performed by multiplying each component of the first vector is to be crossed with each component of the second vector. The cross products of unit vectors are to be performed applying right-hand rule as follows:

\[(\hat i a_x \times \hat i b_x)= a_xb_x(\hat i\times \hat i) = 0\] \[(\hat i a_x \times \hat j b_y)= a_xb_y(\hat i\times \hat j) = a_xb_y\hat k\] \[(\hat i a_x \times \hat k b_z)= a_xb_z(\hat i\times \hat k) = -a_xb_z\hat j\]

\[(\hat j a_y \times \hat i b_x)= a_yb_x(\hat j\times \hat i) = -a_yb_x\hat k\] \[(\hat j a_y \times \hat j b_y)= a_yb_y(\hat j\times \hat j) = 0\] \[(\hat j a_y \times \hat k b_z)= a_yb_z(\hat j\times \hat k) = a_yb_z\hat i\]

\[(\hat k a_z \times \hat i b_x)= a_zb_x(\hat k\times \hat i) = a_zb_x\hat j\] \[(\hat k a_z \times \hat j b_y)= a_zb_y(\hat k\times \hat j) = -a_zb_y\hat i\] \[(\hat k a_z \times \hat k b_z)= a_zb_z(\hat k\times \hat k) = 0\]

The above multiplication can be easily performed using the following determined method:

\[\mathbf{(\vec a \times \vec b)} = \left(\begin{array} {rrr} \hat i & \hat j & \hat k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \\ \end{array}\right) \] $(\vec a \times \vec b) = \hat i (a_yb_z-a_zb_y) - \hat j (a_xb_z-a_zb_x) + \hat k (a_xb_y-a_yb_x)$

Solved Problems:Motion Along a Straight Line

[9] Two vectors are given by $\vec a = (4.0m)\hat i - (3.0m)\hat j+ (1.0m)\hat k$ and $\vec b = (-1.0m)\hat i + (1.0m)\hat j+ (4.0m)\hat k$.

In unit-vector notation, find (a) $\vec a + \vec b$ (b) $\vec a - \vec b$ and (c) a third $\vec c$ vector such that $\vec a - \vec b + \vec c = 0$.

[15] The two vectors $\vec a$ and $\vec b$ in Fig. 3-11 have equal magnitudes of 10.0 m and the angles are $\theta_1= 30^\circ$ and $\theta_2= 105^\circ$. Find the (a) x and (b) y components of their vector sum $\vec r$, (c) the magnitude of $\vec r$, and (d) the angle $\vec r$ makes with the positive direction of the x axis.
[17] Three vectors $\vec a$, $\vec b$, and $\vec c$ each have a magnitude of 50 m and lie in an xy plane. Their directions relative to the positive direction of the x axis are $30^\circ$,$195^\circ$, and $315^\circ$, respectively. What are (a) the magnitude and (b) the angle of the vector $\vec a + \vec b + \vec c$, and (c) the magnitude and (d) the angle of $\vec a - \vec b + \vec c$? What are the (e) magnitude and (f) angle of a fourth vector $\vec d$ such that $(\vec a + \vec b) - (\vec c + \vec d)$?
[31] In Fig. 3-12, a vector with a magnitude of 17.0 m is directed at angle $\theta = 56.0^\circ$ counterclockwise from the +x axis. What are the components (a) $a_x$ and (b) $a_y$ of the vector? A second coordinate system is inclined by angle $\theta'=18.0^\circ$ with respect to the first. What are the components (c) $a_x'$ and (d) $a_y'$ in this primed coordinate system?
[32] In Fig. 3-13, a cube of edge length a sits with one corner at the origin of an xyz coordinate system. A body diagonal is a line that extends from one corner to another through the center. In unit-vector notation, what is the body diagonal that extends from the corner at (a) coordinates (0, 0, 0), (b) coordinates (a, 0, 0), (c) coordinates (0, a, 0), and (d) coordinates (a, a, 0)? (e) Determine the angles that the body diagonals make with the adjacent edges. (f) Determine the length of the body diagonals in terms of a.
[33] For the vectors in Fig. 3-14, with a = 4, b = 3, and c = 5, what are (a) the magnitude and (b) the direction of $\vec a \times \vec b$, (c) the magnitude and (d) the direction of $\vec a \times \vec c$, and (e) the magnitude and (f) the direction of $\vec b \times \vec c$? (The z axis is not shown.)
[35] Two vectors, $\vec r$ and $\vec s$, lie in the xy plane.Their magnitudes are 4.50 and 7.30 units, respectively, and their directions are $320^\circ$ and $85.0^\circ$, respectively, as measured counterclockwise from the positive x axis. What are the values of (a) $\vec r \cdot \vec s$ and (b) $\vec r \times \vec s$?
[37] Three vectors are given by $\vec a = 3.0\hat i + 3.0\hat j - 2.0\hat k$, $\vec b = -1.0\hat i - 4.0\hat j + 2.0\hat k$ and $\vec c = 2.0\hat i + 2.0\hat j - 1.0\hat k$. Find (a) $\vec a \cdot (\vec b \times \vec c)$, (b) $\vec a \cdot (\vec b + \vec c)$ and $\vec a\times(\vec b + \vec c)$.

Problems:Motion Along a Straight Line

Section 3-1 Vectors and Their Components

[3] The x component of vector is 25.0 m and the y component is 40.0 m. (a) What is the magnitude of ? (b) What is the angle between the direction of and the positive direction of x?
[7] Consider two displacements, one of magnitude 3 m and another of magnitude 4 m. Show how the displacement vectors may be combined to get a resultant displacement of magnitude (a) 7 m, (b) 1 m, and (c) 5 m.

Section 3-2 Unit Vectors, Adding Vectors by Components

[10] Find the (a) x, (b) y, and (c) z components of the sum of the displacements and whose components in meters are $c_x = 7.4$, $c_y = 3.8$, $c_z = 6.1$; $d_x = 4.4$, $d_y = 2.0$, $d_z = 3.3$.
[11] (a) In unit-vector notation, what is the sum $\vec a + \vec b$ if $\vec a = (4.0 m)\hat i + (3.0 m)\hat j$ and $\vec b = (-13.0 m)\hat i + (7.0 m)\hat j$? What are the (b) magnitude and (c) direction of $(\vec a + \vec b)$?
[18] In the sum $\vec A + \vec B = \vec C$, vector $\vec A$ has a magnitude of 12.0 m and is angled $40.0^\circ$ counterclockwise from the +x direction, and vector $\vec C$ has a magnitude of 15.0 m and is angled $20.0^\circ$ counterclockwise from the -x direction. What are (a) the magnitude and (b) the angle (relative to +x) of $\vec B$?
[30] Here are two vectors: $\vec a = (4.0 m)\hat i-(3.0 m)\hat j ~~and~~ \vec b = (6.0 m)\hat i+(8.0 m)\hat j$. What are (a) the magnitude and (b) the angle (relative to $\hat i$) of $\vec a$? What are (c) the magnitude and (d) the angle of $\vec b$? What are (e) the magnitude and (f) the angle of $\vec a + \vec b$; (g) the magnitude and (h) the angle of $\vec b - \vec a$; and (i) the magnitude and ( j) the angle of $\vec a-\vec b$? (k) What is the angle between the directions of $\vec b-\vec a$ and $\vec a - \vec b$?

Section 3-3 Multiplying Vectors

[34] Two vectors are presented as $\vec a = 3.0\hat i+5.0\hat j$ and $\vec b = 2.0\hat i+4.0\hat j$. Find (a) $\vec a \times \vec b$, (b) $\vec a \cdot \vec b$, (c) $(\vec a + \vec b)\cdot \vec b$ and (d) the component of $\vec a$ along the direction of $\vec b$. (Hint: For (d), consider Eq. 3-18 and Fig. 3-9.)
[44] In the product $\vec F = q\vec v\times\vec B$, take q = 2, \[\vec v = 2.0\hat i + 4.0 \vec j + 6.0 \vec k~~and~~\vec F = 4.0\hat i - 20.0 \vec j + 12.0 \vec k\]. What then $\vec B$ is in unit-vector notation if $B_x = B_y$?