Chapter 5 Force & Motion-I

Learning Objectives:

In this chapter you will basically learn:

$\bullet$ Learn how the Newtonian Mechanics distinguishes from Relativistic Mechanics and Quantum Mechanics.

$\bullet$ Learn Newton’s first law that applies to a point object that moves in a straight-line with a constant speed with no acceleration or with no net force. This condition applies to a special frames of reference called inertial frames.

$\bullet$ Learn Newton’s second law that applies to a special frames of reference called inertial frames as the change of motion of an object is proportional to the force applied upon it, and is made in the direction of the straight-line in which the force is applied.

$\bullet$ Learn that a force is a vector quantity and has both magnitude and direction and also components. Also, learn how two or more forces acting on the same particle, can be added vectorially to get the net force.

$\bullet$ Learn also Newton’s third law how to every action there is always an equal and opposite reaction.

$\bullet$ Learn how to draw a free-body diagram for an object, showing the object as a particle with the forces acting on it as vectors with their tails anchored on the particle.

$\bullet$ Learn how to apply the Newton’s second law between the net force on an object, the mass of the object, and the acceleration produced by the net force.

$\bullet$ Learn how to calculate the magnitude and direction of the gravitational force acting on a body with a given mass, in free-fall acceleration.

$\bullet$ Learn that a scale or a weighing machine gives an object’s weight when the measurement is done in an inertial frame but not in an accelerating frame, where it gives an apparent weight.

$\bullet$ Learn how to calculate the magnitude and direction of the normal force on an object when the object is pressed or pulled onto a surface.

$\bullet$ Learn that the force parallel to the surface is a frictional force that appears when the object slides or attempts to slide along the surface.

$\bullet$ Identify that a tension force is said to pull at both ends of a cord (or a cord-like object) when the cord is taut.

5.1 Newtonian Mechanics:

Newtonian mechanics describes and predict the motions of the planets and stars including the motions of planets and satellites in and around Earth and Sun. The general principles and the mathematical models that were used to describe the motions of planets and stars first formulated by Sir Isaac Newton in a book entitled “Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy)”. This book, was first published in 1687.

Newton’s theory and mathematical models were assumed to be a comprehensive and complete description of all types of motion occurring in the heavenly bodies as well as motions in the man made devices. In the beginning of the 20th century, physicists started realizing that Newtonian mechanics is based on Euclidean geometry just an approximation fails in regions of space which are sufficiently curved. In a curved space where Euclidean geometry do not hold to a good approximation, and must be replaced and described by Einstein’s general theory of relativity.

General relativity errors are so small that Einstein had difficulty finding a place where the deviations from Newtonian mechanics could be observed at all occur due to space-time curvature. Newtonion mechanics predicts a fixed eliptical orbit. Einstein’s equations correctly predicted that the eliptical path itself rotates (precesses) once every 3 million years, that’s about 45 arcsec (an 80th of a degree) per century. So the Newtonian ‘error’ is about one part in $10^8$. Finally Eistein predicted a small, barely measurable effect on the predicted motion of the planet Mercury. Global positioning system (GPS) take general relativity into consideration to correct errors of about one part in a billion (a millimeter error over a thousand kilometers).

Newtonian mechanics also fails to hold when the velocities of the objects under investigation approach the speed of light in vacuum, and must be modified in accordance with Einstein’s special theory of relativity. The errors from neglecting the effects of special relativity are on the order of $\frac{v^2}{c^2}$ where v is the speed of the object in consideration and c is the speed of light. The maximum errors are associated with the fastest objects. As an example we can calculate the error that occurs in the space shuttle orbiting around the Earth. The error can be calculated to be

\[\frac{v^2}{c^2}=\left(\frac{8.05\times 10^3 ~m/s}{3.0\times 10^8 ~m/s}\right)^2=0.72\times 10^{-9}\approx 1.0\times 10^{-9}\]

one millionth of one percent which is negligibly small.

Newtonian mechanics also fails to describe the motion of atomic and subatomic particles where we apply quantum mechanics.

In classical mechanics we can measure exactly where an object is and how fast it is moving. But in case of subatomic particles it is not possible to measure the particle’s position without measurement uncertainty. The product of the uncertainty $\delta x$ in position of an object and the the uncertainty $\delta p$ of its momentum must be greater than Planck’s constant $\hslash$. Considering the Planck’s constant value is $\hslash$ =$1.05\times10^{-34}$ joule-s. The fractional error in position is biggest for small objects moving slowly. So if one measures the location of an object with mass $m = 10^{-4}$ kg to within $\delta x = 10^{-6}$ m $\approx$ a twenty fifth of a thousands of an inch, the uncertainty in its velocity $\delta v = \frac{\delta p}{m}$ is only $\delta x\delta p = \hslash$

\[\delta v = \frac{m\hslash}{\delta x} \simeq 10^{-24}~m/s \simeq 10^{-15} ~inches~ per~ year.\]

Considering the above analysis, in this chapter we neglect both relativistic and quantum effects including the effect of frictional force in the system. We therefore restrict our discussion to the motions of large objects (compared to an atom) with speeds much lower than to the speed of light objects moving in Euclidean space.

Newtonian mechanics holds true for the motions which we commonly observe and encounter in the world around us. The results based on the ideas of position as a function of time in space, can be correctly described by the Euclidean vector algebra and vector calculus.

Newtonian mechanics make use of the fundamental quantities of mass, position, time, and force to formulate the Euclidean algebra. In describing the Newtonian mechanics, the axioms are called Newton’s laws of motion, and can only be verified by experimental results. Also, assumptions are made that Newton’s laws, are only applicable to point objects but can be applied to extended objects by treating them as collections of point objects.

5.1.1 Newton’s First Law of Motion:

Newton’s first law of motion, as described in the Principia, may be described as: Every object stays in its state of rest, or move in a uniform motion in a straight-line, unless it is compelled to change that state by forces imposed upon it.

Newton’s first law applies to a point object with zero net external force that moves in a straight-line with a constant speed with no acceleration or with no net force. This condition applies to a special frames of reference called inertial frames. Or in other words Newton’s first law holds in an inertial frame of reference in which a point object subject to zero net external force moves in a straight-line with constant speed.

In a Cartesian coordinate system we assume an inertial frame of reference. The motion of a point object can now be specified by giving its position vector, with respect to the origin of the coordinate system, as a function of time, $t$.

\[\begin{equation} {\vec r(t)}\equiv \hat ix(t) + \hat jy (t)+\hat kz(t) \tag{5.1} \end{equation}\]

Consider a second frame of reference moving with some constant velocity ${\vec u}$ with respect to the first frame. We also assume that the Cartesian axes in both the frames are parallel to each other, that ${\vec u} \equiv (u_x,0,0)$, and the origins of the two frames instantaneously coincide at $t=0$ as can be seen in Figure 5-1.

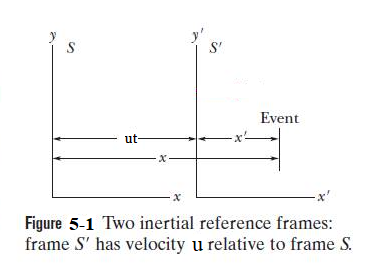
Suppose that the position vector of our point object is ${\vec r}'\equiv (\hat ix' + \hat j\,y'+\hat k\,z')$,in the second frame of reference. It is evident, from Figure 1, that at any given time, $t$, the coordinates of the object in the two reference frames satisfy

\[\begin{equation} x' = x-ut \tag{5.2} \end{equation}\]

\[\begin{equation} y' = y \tag{5.3} \end{equation}\]

\[\begin{equation} z' = z \tag{5.4} \end{equation}\]

This coordinate transformation as shown in Figure 5-1 was first discovered by Galileo Galilei, and by his name it is known as a Galilean transformation.

The instantaneous velocity of the object in our first reference frame is given by

\[\begin{equation} \vec v = \frac{d\vec r}{dt} \equiv (\hat i\frac{dx}{dt} + \hat j\frac{dy}{dt} + \hat k\frac{dz}{dt}) \equiv (\hat iv_x + \hat jv_y + \hat kv_z), \tag{5.5} \end{equation}\]

with an analogous expression for the velocity, in the second frame.

\[\begin{equation} {\vec v}'= \frac{d\vec r'}{dt} \equiv (\hat i\frac{dx'}{dt} + \hat j\frac{dy'}{dt} + \hat k\frac{dz'}{dt})\equiv (\hat iv_x' + \hat jv_y' + \hat kv_z'), \tag{5.6} \end{equation}\]

It follows from differentiation of Equations (5-2)-(5-4) with respect to time that the components in the two frames satisfy

\[\begin{equation} v_x'=v_x - u, \tag{5.7} \end{equation}\]

\[\begin{equation} v_y'=v_y , \tag{5.8} \end{equation}\]

\[\begin{equation} v_z'=v_z , \tag{5.9} \end{equation}\]

These equations can be written in a vectorial form as follows:

\[\begin{equation} \vec v' = \vec v - \vec u. \tag{5.10} \end{equation}\]

By taking one more derivatives of Eq.5-5 and 5-6 the instantaneous acceleration components of the object with respect to the first reference frame is given by

\[\begin{equation} {\vec a} = \frac{d\vec v}{dt} \equiv \left(\hat i \frac{dv_x}{dt}+\hat j\frac{dv_y}{dt}+\hat k\frac{dv_z}{dt}\right) \equiv (\hat ia_x + \hat ja_y + \hat ka_z), \tag{5.11} \end{equation}\]

with an analogous expression for the acceleration, $\vec a'$, in the second frame. It follows from differentiation of Equations (4)-(6) with respect to time that the acceleration components in the two frames satisfy

\[\begin{equation} {\vec a'} = \frac{d\vec v'}{dt} \equiv \left(\hat i \frac{dv_x'}{dt}+\hat j\frac{dv_y'}{dt}+\hat k\frac{dv_z'}{dt}\right) \equiv (\hat ia_x' + \hat ja_y' + \hat ka_z'), \tag{5.12} \end{equation}\]

These equations can be written in a vector form \[\begin{equation} \vec a' = \vec a. \tag{5.13} \end{equation}\]

According to Equations (5-10) and (5-13), if an object is moving in a straight-line with constant speed in the first inertial frame (i.e., if $\vec a=0$) then it also move in a (different) straight-line with (a different) constant speed in the second frame of reference (i.e., $\vec a'= 0$). Hence, we conclude that the second frame of reference is also an inertial frame.

A simple extension of the above argument allows us to conclude that there are an infinite number of different inertial frames moving with constant velocities with respect to one another. Newton thought that one of these inertial frames was special, and defined an absolute standard of rest: i.e., a static object in this frame was in a state of absolute rest. However, Einstein showed that this is not the case. In fact, there is no absolute standard of rest: i.e., all motion is relative–hence, the name “relativity” for Einstein’s theory. Consequently, one inertial frame is just as good as another as far as Newtonian mechanics is concerned.

But, what happens if the second frame of reference accelerates with respect to the first? In this case, it is not hard to see that Equation (5-13) generalizes to

\[\begin{equation} {\vec a'} = {\vec a} - \frac{d{\vec u}}{dt}, \tag{5.14} \end{equation}\]

where ${\vec u}(t)$ is the instantaneous velocity of the second frame with respect to the first. According to the above formula, if an object is moving in a straight-line with constant speed in the first frame (i.e., if ${\vec a}={\bf0}$) then it does not move in a straight-line with constant speed in the second frame (i.e., ${\bf a}'\neq{\bf0}$). Hence, if the first frame is an inertial frame then the second is not.

A simple extension of the above argument allows us to conclude that any frame of reference which accelerates with respect to a given inertial frame is not itself an inertial frame.

For most practical purposes, when studying the motions of objects close to the Earth’s surface, a reference frame which is fixed with respect to Earth’s surface is approximately inertial. However, if the trajectory of a projectile within such a frame is measured to high precision then it will be found to deviate slightly from the predictions of Newtonian mechanics.

This deviation is due to the fact that the Earth is rotating, and its surface is therefore accelerating towards its axis of rotation. The effect of Earth’s rotation on its own axis has the most effect in the equator and can be found using $\left(g = a_g-\omega^2R\right)$. In the equator $g$ is less than $a_g$ by only about $0.034 ~\frac{m}{s^2}$ which is small compared to $g = 9.8~\frac{m}{s^2}$.

Considering the motions of objects in orbit around the Earth, a reference frame whose origin is the center of the Earth, and whose coordinate axes are fixed with respect to distant stars, is approximately inertial. However, if such orbits are measured to extremely high precision then they will again be found to deviate very slightly from the Newtonian mechanics.

In this case, the deviation is due to the Earth’s centripetal acceleration about the Sun can be found using $a = \frac{GM_s}{R^2}$, where R is the distance between Earth and Sun $\left(R=1.50\times 10^{11}~m\right)$, and $G=6.67\times 10^{-11}\frac{m^3}{kg-s^2}$.

The acceleration that Earth experiences rotating around the Sun is approximately equal to:

\[a=\left(\frac{GM_s}{R^2}\right) =\frac{\left(6.67\times 10^{-11}\frac{m^3}{kg-s^2}\right) \left(1.99\times 10^{30} kg\right)}{\left(1.50\times 10^{11}~m\right)^2}=0.005899\frac{m}{s^2}\]

When studying the orbits of the planets in the Solar System, a reference frame whose origin is the center of the Sun, and whose coordinate axes are fixed with respect to distant stars, is approximately inertial. In this case, any deviations of the orbits from the predictions of Newtonian mechanics is due to the orbital motion of the Sun about the galactic center are far too small to be measurable. It should be noted that it is impossible to identify an absolute inertial frame–the best approximation to such a frame would be one in which the cosmic microwave background appears to be (approximately) isotropic. However, for a given dynamical problem, it is always possible to identify an approximate inertial frame. Furthermore, any deviations of such a frame from a true inertial frame can be incorporated into the framework of Newtonian mechanics via the introduction of so-called fictitious forces.

5.1.2 Newton’s Second Law of Motion:

The change of motion (i.e., momentum) of an object is proportional to the force applied upon it, and is made in the direction of the straight-line in which the force is applied.

Newton’s second law of motion essentially states that if a point object is subject to an external force, ${\vec F}$, then its equation of motion is given by

\[\begin{equation} {\vec F_{net}} = \frac{d{\vec p}}{dt} \tag{5.15} \end{equation}\]

where the momentum, ${\vec p}$, is the product of the object’s inertial mass, $m$, and its velocity, ${\vec v}$. If $m$ is not a function of time then the above expression reduces to the familiar equation

\[\begin{equation} m\frac{d{\vec v}}{dt} = {\vec F_{net}} \tag{5.16} \end{equation}\]

Note that this equation is only valid in an inertial frame. Clearly, the inertial mass of an object measures its reluctance to deviate from its preferred state of uniform motion in a straight-line (in an inertial frame). Of course, the above equation of motion can only be solved if we have an independent expression for the force, ${\vec F}$ (i.e., a law of force).

Taking the scalar product of Eq.5-16 with the velocity, ${\bf v}$, we obtain

\[\begin{equation} m\vec v\cdot\frac{d {\vec v}}{dt} = \frac{m}{2}\frac{d\vec v.\vec v}{dt}=\frac{m}{2}\frac{d v^2}{dt} =\frac{dK}{dt}= \vec F\cdot\vec v \tag{5.17} \end{equation}\]

This can be written

\[\begin{equation} \frac{d K}{dt} = {\vec F}\cdot {\vec v} \tag{5.18} \end{equation}\]

where

\[\begin{equation} K = \frac{1}{2}\,m\,v^2 \tag{5.19} \end{equation}\]

The quantity $K$ represents the energy of the object gains by its motion and is known as kinetic energy. Thus, Eq. 5-19 states that any work done on point object by an external force goes to increase the object’s kinetic energy.

Suppose that, under the action of the force, $\vec F$, the object moves from point $P$ at time $t_1$ to point $Q$ at time $t_2$. The net change in the object’s kinetic energy is obtained by integrating Eq. 5-18:

\[\begin{equation} \Delta K = \int_{t_1}^{t_2} {\vec F}\cdot{\vec v}dt =\int_P^Q {\vec F}\cdot d{\vec r} \tag{5.20} \end{equation}\]

since $\vec v = \frac{d\vec r}{dt}$. Here, $d{\vec r}$ is an element of the object’s path between points $P$ and $Q$, and the integral in Eq. 5-20 represents the net work done by the force as the objects moves along the path from $P$ to $Q$.

There are two kinds of forces that we encounter namely conservative and non-conservative. If line integral of $\int_P^Q {\vec F}\cdot d{\vec r}$ depends on the end points, but not on the path taken between these points it is called conservative force. On the other hand, if the line integral of the type $\int_P^Q {\vec F}\cdot d{\vec r}$ depends both on the end points, and the path taken between these points it is called non-conservative force. In other words, all conservative forces satisfy

\[\begin{equation} {\vec F} = - \nabla U \tag{5.21} \end{equation}\]

for some scalar field $U({\vec r})$ is called potential energy. Note that

\[\begin{equation} \int_P^Q \nabla \vec U\cdot d{\vec r} \equiv \Delta U = U(Q) - U(P) \tag{5.22} \end{equation}\]

irrespective of the path taken between $P$ and $Q$. Hence, it follows from Eq. 5-20 that

\[\begin{equation} {\mit\Delta} K = - {\mit\Delta} U \tag{5.23} \end{equation}\]

for conservative forces. Another way of writing this is

\[\begin{equation} E = K + U = {\rm constant} \tag{5.24} \end{equation}\]

In Eq. 5-24, E is the total energy is the sum of kinetic and potential energies remain constant for a conservative force.

Gravitational force is a conservative force and frictional force is an example of non-conservative force.

Newton’s second law in a simplistic form can be written as:

5.1.3 Newton’s Third Law of Motion:

To every action there is always an equal and opposite reaction. The mutual actions of two bodies upon each other are always equal and directed to opposite to each other.

Consider a system of $N$ mutually interacting point objects. Let the $i$th object, whose mass is $m_i$, be located at vector displacement ${\vec r}_i$. Suppose that this object exerts a force ${\vec F}_{ji}$ on the $j$th object. Likewise, suppose that the $j$th object exerts a force ${\vec F}_{ij}$ on the $i$th object. Newton’s third law of motion essentially states that these two forces are equal and opposite, irrespective of their nature. In other words,

\[\begin{equation} {\vec F}_{ij} = - {\vec F}_{ji} \tag{5.25} \end{equation}\]

One corollary of Newton’s third law is that an object cannot exert a force on itself. Another corollary is that all forces in the Universe have corresponding reactions. The only exceptions to this rule are the fictitious forces which arise in non-inertial reference frames (e.g., the centrifugal and Coriolis forces which appear in rotating reference frames–see Chapter 7). Fictitious forces do not possess reactions. It should be noted that Newton’s third law implies action at a distance. In other words, if the force that object $i$ exerts on object $j$ suddenly changes then Newton’s third law demands that there must be an immediate change in the force that object $j$ exerts on object $i$. Moreover, this must be true irrespective of the distance between the two objects. However, we now know that Einstein’s theory of relativity forbids information from traveling through the Universe faster than the velocity of light in vacuum $\left(c=\frac{1}{\sqrt{\epsilon_0\mu_0}}=3\times 10^8\frac{m}{s}\right)$. The upper bound of the propagation of light is being restricted by the electric and magnetic nature of the space. Hence, action at a distance is also forbidden. In other words, if the force that object $i$ exerts on object $j$ suddenly changes then there must be a time delay, which is at least as long as it takes a light ray to propagate between the two objects, before the force that object $j$ exerts on object $i$ can respond. Of course, this means that Newton’s third law is not, strictly speaking, correct. However, as long as we restrict our investigations to the motions of dynamical systems on time-scales that are long compared to the time required for light-rays to traverse these systems, Newton’s third law can be regarded as being approximately correct.

In an inertial frame, Newton’s second law of motion applied to the $i$th object yields

\[\begin{equation} m_i\,\frac{d^2 {\vec r}_i}{dt^2} = \sum_{j=1,N}^{j\neq i}\! {\vec F}_{ij} \tag{5.26} \end{equation}\]

Note that the summation on the right-hand side of the above equation excludes the case $j=i$, since the $i$th object cannot exert a force on itself. Let us now take the above equation and sum it over all objects. We obtain

\[\begin{equation} \sum_{i=1,N} \!m_i\,\frac{d^2 {\bf r}_i}{dt^2}=\sum_{i,j=1,N}^{j\neq i}\! {\vec F}_{ij} \tag{5.27} \end{equation}\]

Consider the sum over forces on the right-hand side of the above equation. Each element of this sum–${\vec F}_{ij}$, say–can be paired with another element–${\vec F}_{ji}$, in this case–which is equal and opposite, according to Newton’s third law. In other words, the elements of the sum all cancel out in pairs. Thus, the net value of the sum is zero. It follows that the above equation can be written

\[\begin{equation} M\,\frac{d^2 {\vec r}_{cm}}{dt^2}= {\vec0} \tag{5.28} \end{equation}\]

where $M = \sum_{i=1}^N m_i$ is the total mass. The quantity ${\vec r}_{cm}$ is the vector displacement of the center of mass of the system, which is an imaginary point whose coordinates are the mass weighted averages of the coordinates of the objects that constitute the system: i.e.,

\[\begin{equation} {\vec r}_{cm} = \frac{\sum_{i=1}^N m_i\,{\vec r}_i}{\sum_{i=1}^N m_i} \tag{5.29} \end{equation}\]

According to Equation , the center of mass of the system moves in a uniform straight-line, in accordance with Newton’s first law of motion, irrespective of the nature of the forces acting between the various components of the system. Now, if the center of mass moves in a uniform straight-line then the center of mass velocity,

\[\begin{equation} \frac{d{\vec r}_{cm} }{dt}= \frac{\sum_{i=1}^N m_i\, d{\vec r}_i/dt}{\sum_{i=1}^N m_i} \tag{5.30} \end{equation}\]

is a constant of the motion. However, the momentum of the $i$th object takes the form ${\vec p}_i = m_i\,d{\vec r}_i/dt$. Hence, the total momentum of the system is written

\[\begin{equation} {\bf P} = \sum_{i=1}^N m_i\,\frac{d {\vec r}_i}{dt} \tag{5.31} \end{equation}\]

A comparison of Equations (28) and (29) suggests that ${\vec P}$ is also a constant of the motion. In other words, the total momentum of the system is a conserved quantity, irrespective of the nature of the forces acting between the various components of the system. This result (which only holds if there is no net external force acting on the system) is a direct consequence of Newton’s third law of motion. Taking the vector product of Equation (24) with the position vector $\vec r_i$, we obtain

\[\begin{equation} m_i\vec r_i\times \frac{d^2 \vec r_i}{dt^2}= \sum_{j=1,N}^{j\neq i} \vec r_i\times \vec F_{ij} \tag{5.32} \end{equation}\]

However, it is easily seen that

\[\begin{equation} m_i\vec r_i\times \frac{d^2 \vec r_i} {dt^2}= \frac{d}{dt}\left(m_i\vec r_i\times \frac{d \vec r_i}{dt}\right) = \frac{d \vec l_i}{dt} \tag{5.33} \end{equation}\]

where

\[\begin{equation} {\vec l}_i = m_i\,{\vec r}_i\times \frac{d{\vec r}_i}{dt} \tag{5.34} \end{equation}\]

is the angular momentum of the $i$th particle about the origin of our coordinate system. The total angular momentum of the system (about the origin) takes the form

\[\begin{equation} {\vec L} = \sum_{i=1,N} {\vec l}_i \tag{5.35} \end{equation}\]

Hence, summing Equation (30) over all particles, we obtain

\[\begin{equation} \frac{d {\vec L}}{dt} = \sum_{i,j = 1,N}^{i\neq j} {\vec r}_i\times {\vec F}_{ij} \tag{5.36} \end{equation}\]

Consider the sum on the right-hand side of the above equation. A general term, ${\vec r}_i\times {\vec F}_{ij}$, in this sum can always be paired with a matching term, ${\vec r}_j\times {\vec F}_{ji}$, in which the indices have been swapped. Making use of Equation (23), the sum of a general matched pair can be written

\[\begin{equation} {\vec r}_i\times {\vec F}_{ij}+{\vec r}_j\times {\vec F}_{ji} = ({\vec r}_i-{\vec r}_j)\times {\vec F}_{ij} \tag{5.37} \end{equation}\]

Let us assume that the forces acting between the various components of the system are central in nature, so that ${\vec F}_{ij}$ is parallel to ${\vec r}_i-{\vec r}_j$. In other words, the force exerted on object $j$ by object $i$ either points directly toward, or directly away from, object $i$, and vice versa. This is a reasonable assumption, since most of the forces which we encounter in the world around us are of this type (e.g., gravity). It follows that if the forces are central in nature then the vector product on the right-hand side of the above expression is zero. We conclude that

\[\begin{equation} {\vec r}_i\times {\vec F}_{ij}+{\vec r}_j\times {\vec F}_{ji} = {\vec0} \tag{5.38} \end{equation}\]

for all values of $i$ and $j$. Thus, the sum on the right-hand side of Equation is zero for any kind of central force. We are left with

\[\begin{equation} \frac{d {\vec L}}{dt} = {\vec0} \tag{5.39} \end{equation}\]

In other words, the total angular momentum of the system is a conserved quantity, provided that the different components of the system interact via central forces (and there is no net external torque acting on the system).

5.2 Force & Mass:

Solved Problems:Force & Motion-I

[7] There are two forces on the 2.00 kg box in the overhead view of Fig. 5-31, but only one is shown. For $F_1 = 20.0 N$, $a = 12.0 m/s^2$, and $\theta = 30.0^\circ$, find the second force (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the x axis.

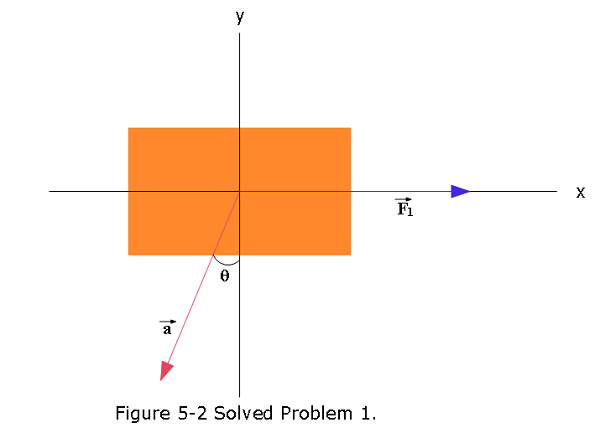
Solution: (a) $\vec F_{net}=m\vec a$ \[\vec F_1 + \vec F_2 = m\vec a\] \[\vec F_2 = m\vec a -\vec F_1\] \[F_{2,x}=-ma\sin30^\circ-F_{1,x}=-(2~kg)(12.0~m/s^2)\sin30^\circ-20.0 = -32~N\] \[F_{2,y}=-ma\cos30^\circ-F_{1,y}=-(2~kg)(12.0~m/s^2)\cos30^\circ-0 = -20.78~N\] \[\vec F_2=-(32~N)\hat i -(20.78~N)\hat j\space (Answer)\]

Magnitude of force $|\vec F_2|=\sqrt{(-32~N)^2+(-20.78~N)^2}=38.16~N\space(Answer)$
Direction relative to x-axis: $\theta = tan^{-1}\left(\frac{20.78}{32}\right)=32.99^\circ\space(Answer)$ \[32.99^\circ-180^\circ=-147^\circ\]

[9] A 0.340 kg particle moves in an xy plane according to $x(t)= -15.00 + 2.00t -4.00t^3$ and y(t) = 25.00 + 7.00t - 9.00t^2$, with x and y in meters and t in seconds. At t = 0.700 s, what are (a) the magnitude and (b) the angle (relative to the positive direction of the x axis) of the net force on the particle, and (c) what is the angle of the particle’s direction of travel?

Solution:

$v_x=\frac{d}{dt} (-15+2.0~t-4.00~t^3)=2.0-12.0t^2$

$a_x=\frac{d}{dt}(2.0-12.0t^2)=-24.0t$

$v_y=\frac{d}{dt} (25.00+7.0~t-9.00~t^2)=7.00-18.0t$

$a_y=\frac{d}{dt}(7.0-18.0t)=-18.0$

At t = 0.70 s

$a=\sqrt{[(-24.0)(0.7~s)]^2+(-18)^2}=24.62~m/s^2$

$F = ma = (0.34~kg)(24.62~m/s^2)=8.37~N\space(Answer)$ (b) $\theta_a=tan^{-1}(\frac{-18}{-16.8})=46.97^\circ$

$46.97^\circ-180^\circ=-133^\circ\space(Answer)$

$v_x(t=0.70~s)=2.0-12.0(0.70~s)^2=-3.88~m/s$

$v_y=7.00-18.0(0.70~s)=-5.6~m/s$

$\theta_v=tan^{-1}(\frac{-5.6~m/s}{-3.88~m/s})=55.28^\circ$

$55.28^\circ-180^\circ=-124.72^\circ\space(Answer)$

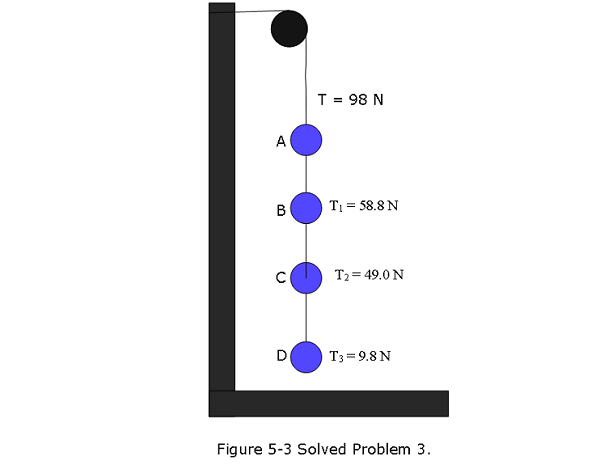
[13] Figure 5-3 shows an arrangement in which four disks are suspended by cords.The longer, top cord loops over a frictionless pulley and pulls with a force of magnitude 98 N on the wall to which it is attached. The tensions in the three shorter cords are $T_1$ = 58.8 N, $T_2$ = 49.0 N, and $T_3$ = 9.8 N. What are the masses of (a) disk A, (b) disk B, (c) disk C, and (d) disk D?

Solution:

Mass of disk A: \[\Sigma F_y = 0\] \[T-T_1-m_Ag=0\] \[m_A=\frac{T-T_1}{g}=\frac{98~N-58.8~N}{9.8~m/s^2}=4~kg\space(Answer)\]
Mass of disk B: \[\Sigma F_y = 0\] \[T_1-T_2-m_Bg=0\] \[m_B=\frac{T_1-T_2}{g}=\frac{58.8~N-49.0~N}{9.8~m/s^2}=1~kg\space(Answer)\]
Mass of disk C: \[\Sigma F_y = 0\] \[T_2-T_3-m_Cg=0\] \[m_C=\frac{T_2-T_3}{g}=\frac{49.0~N-9.8~N}{9.8~m/s^2}=4~kg\space(Answer)\]
Mass of disk D: \[\Sigma F_y = 0\] \[T_3-m_Dg=0\] \[m_D=\frac{T_3}{g}=\frac{9.8~N}{9.8~m/s^2}=1~kg\space(Answer)\]

[15] (a) An 11.0 kg mass is supported by a cord that runs to a spring scale, which is supported by a cord hung from the ceiling (Fig. 5-4a).What is the reading on the scale, which is marked in SI weight units? (b) In Fig. 5-4b the mass is supported by a cord that runs around a pulley and to a scale.The opposite end of the scale is attached by a cord to a wall. What is the reading on the scale? (c) In Fig. 5-34c the wall has been replaced with a second 11.0 kg mass, and the assembly is stationary. What is the reading on the scale?

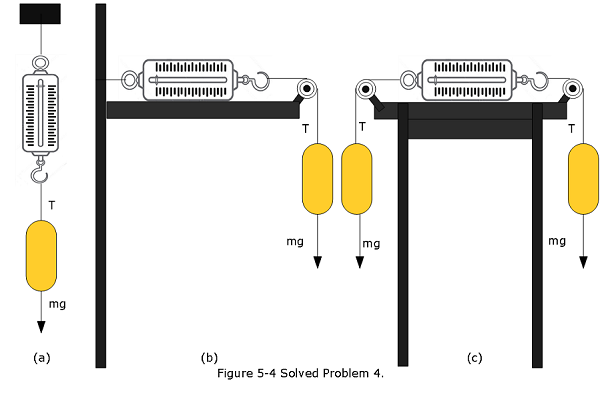
Solution:

Reading on the scale: $T-mg=0$ $T = mg = (11.0~kg)(9.8~kg/s^2=107.8~N\approx 108~N~(Answer)$
Reading on the scale: $T-mg=0$ $T = mg = (11.0~kg)(9.8~kg/s^2=107.8~N\approx 108~N~(Answer)$
Reading on the scale: $2T-2mg=0$ $T = mg = (11.0~kg)(9.8~kg/s^2=107.8~N\approx 108~N~(Answer)$

[17] In Fig. 5-5, let the mass of the block be 8.5 kg and the angle be $30^\circ$. Find (a) the tension in the cord and (b) the normal force acting on the block. (c) If the cord is cut, find the magnitude of the resulting acceleration of the block.

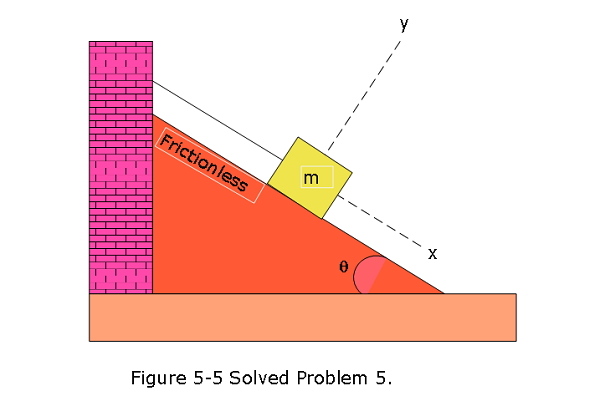
Solution: (a) $\Sigma\vec F_{net}=0$ \[\Sigma F_{net,x}=0\] \[mg\sin\theta-T=0\] \[T=mg\sin\theta=(8.5~kg)(9.8~m/s^2)\sin30\circ=41.65\approx42~N\space(Answer)\]

\[\Sigma F_{net,y}=0\] \[F_N-mg\cos\theta=0\] \[F_N = mg\cos\theta=(8.5~kg)(9.8~m/s^2)\cos30\circ=72.14\approx72~N\space(Answer)\]
Once the cord is cut: \[mg\sin\theta-0=-ma_x\] \[a_x=-g\sin\theta=-9.8~m/s^2\sin30^\circ = -4.9~m/s^2\space (Answer)\]

Minus sign indicating that the acceleration is downward. The magnitude of the acceleration is $a_x=|-4.9~m/s^2|=4.9~m/s^2$

[19] A 500 kg rocket sled can be accelerated at a constant rate from rest to 1600 km/h in 1.8 s.What is the magnitude of the required net force?

Solution:_ Given $v=1600~km/h=\frac{1600\times 10^3~m}{3600~s}=444.44~m/s$ \[v=v_0+at\] Since rocket sled starts from rest, $v_0=0$, acceleration, $a=\frac{v}{t}=\frac{444.44~m/s}{1.8~s}=246.91~m/s^2$

Magnitude of the force: $F=ma=(500~kg)(246.91~m/s^2)=1.23\times10^5~N\space(Answer)$

[21] A constant horizontal force $\vec F_a$ pushes a 2.00 kg FedEx package across a frictionless floor on which an xy coordinate system has been drawn. Figure 5-6 gives the package’s x and y velocity components versus time t. What are the (a) magnitude and (b) direction of $\vec F_a$?

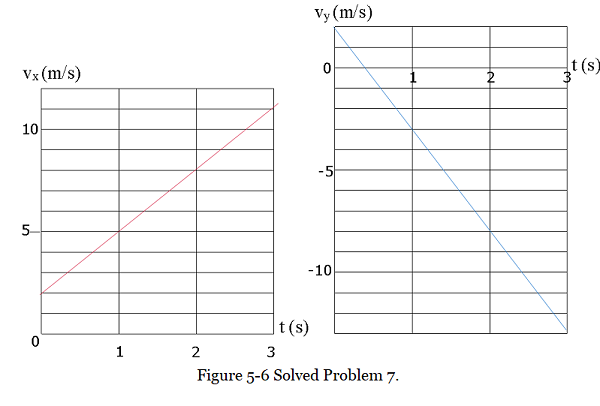
Solution:

\[a_x=\frac{(11-2)m/s}{(3-0)s}=3\space m/s^2\] \[a_y=\frac{(-13-2)m/s}{(3-0)s}=-5\space m/s^2\] \[a=\sqrt{(a_x^2+a_y^2)}=\sqrt{(3m/s)^2+(-5m/s)^2)}=5.83\space m/s^2\]

Magnitude of the force: $F = ma = (2.00\space kg)(5.83\space m/s^2=11.66~N\approx 11.7~N\space (Answer)$
Direction of force: $\theta=tan^-1(5/3)=-59^\circ\space(Answer)$

[59] A 10 kg monkey climbs up a massless rope that runs over a frictionless tree limb and back down to a 15 kg package on the ground (Fig. 5-7). (a) What is the magnitude of the least acceleration the monkey must have if it is to lift the package off the ground? If, after the package has been lifted, the monkey stops its climb and holds onto the rope, what are the (b) magnitude and (c) direction of the monkey’s acceleration and (d) the tension in the rope?

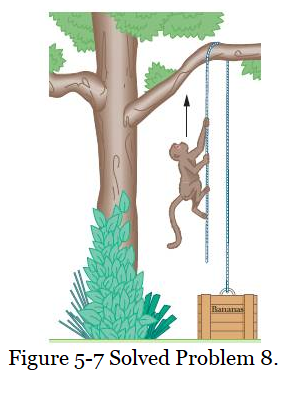
Solution:

$T-m_mg=m_ma~~~~~~~~~~~~(1)$ In order to lift the package tension $T=m_pg$. Substituting $T=m_pg$ in Eq. 1, we can find the monkey’s acceleration as follows: \[a=\frac{g(m_p-m_m)}{m_m}=\frac{(9.8~m/s^2)(15kg-10kg)}{10kg}=4.9~m/s^2\space(Answer)\]
Once monkey stops climbing, monkey will go upward and the package will go downward because it is heavier than the monkey. As a result the monkey will go upward with an acceleration and package will go down with the same acceleration as the monkey downward:

\[T-m_pg = -m_pa~~~~~~~~~~~~(2)\]

Now solving Eqs. (1) and (2), the magnitude of the monkey’s acceleration will become:

\[a = \frac{m_p-m_m)g}{m_m+m_p)}=\frac{(15kg-10kg)(9.8m/s^2)}{(10kg+15kg)}=1.96~m/s^2\space(Answer)\]

Upward
From Eq. 1 or Eq. 2, we can find the tension on the rope:

\[T=m_m(a+g)=10~kg(1.96~m/s^2+9.8~m/s^2)=117~N\]

Problems:Force & Motion-I

Section 5-1 Newton’s First and Second Laws:

[10] A 0.150 kg particle moves along an x axis according to $x(t)=-13.00 + 2.00t + 4.00t^2 - 3.00t^3$, with x in meters and t in seconds. In unit-vector notation, what is the net force acting on the particle at t = 3.40 s?
[11] A 2.0 kg particle moves along an x axis, being propelled by a variable force directed along that axis. Its position is given by $x = 3.0 m + (4.0 m/s)t + ct^2 - (2.0 m/s3)t^3$, with x in meters and t in seconds. The factor c is a constant. At t = 3.0 s, the force on the particle has a magnitude of 36 N and is in the negative direction of the axis. What is c?
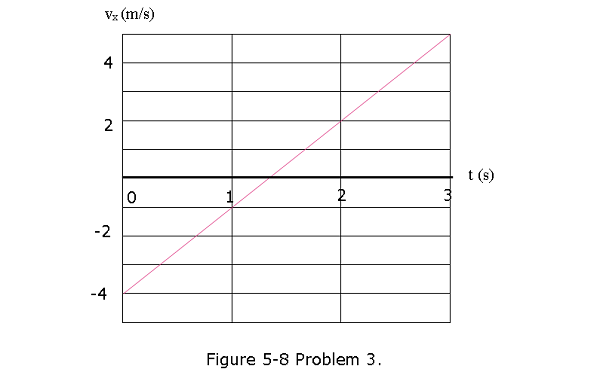
[12] Two horizontal forces $\vec F_1$ and $\vec F_2$ act on a 4.0 kg disk that slides over frictionless ice, on which an xy coordinate system is laid out. Force $\vec F_1$ is in the positive direction of the x axis and has a magnitude of 7.0 N. Force $\vec F_2$ has a magnitude of 9.0 N. Figure 5-8 gives the x component $v_x$ of the velocity of the disk as a function of time t during the sliding. What is the angle between the constant directions of forces $\vec F_1$ and $\vec F_2$?

Section 5-2 Some Particular Forces:

[14] A block with a weight of 3.0 N is at rest on a horizontal surface. A 1.0 N upward force is applied to the block by means of an attached vertical string. What are the (a) magnitude and (b) direction of the force of the block on the horizontal surface?

Section 5-3 Applying Newton’s Laws:

[20] A car traveling at 53 km/h hits a bridge abutment. A passenger in the car moves forward a distance of 65 cm (with respect to the road) while being brought to rest by an inflated air bag.What magnitude of force (assumed constant) acts on the passenger’s upper torso, which has a mass of 41 kg?
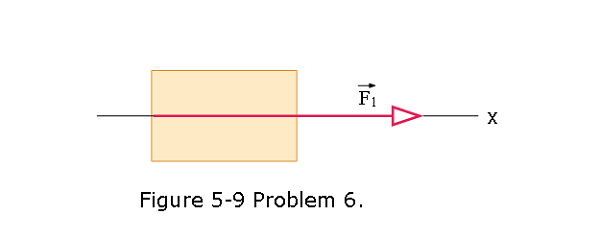
[24] There are two horizontal forces on the 2.0 kg box in the overhead view of Fig. 5-9 but only one (of magnitude $F_1 = 20 N$) is shown. The box moves along the x axis. For each of the following values for the acceleration $a_x$ of the box, find the second force in unit-vector notation: (a) $10 m/s^2$, (b) $20 m/s^2$, (c) 0, (d) -$10 m/s^2$, and (e) -$20 m/s^2$.

[31] A block is projected up a frictionless inclined plane with initial speed $v_0$ = 3.50 m/s. The angle of incline is $\theta = 32.0^\circ$. (a) How far up the plane does the block go? (b) How long does it take to get there? (c) What is its speed when it gets back to the bottom?
[33] An elevator cab and its load have a combined mass of 1600 kg. Find the tension in the supporting cable when the cab, originally moving downward at 12 m/s, is brought to rest with constant acceleration in a distance of 42 m.
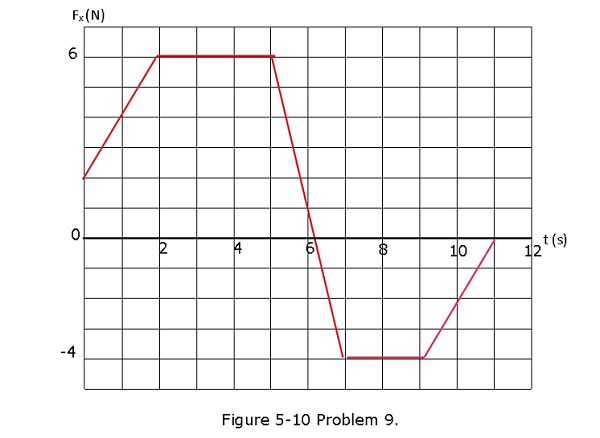
[63] Figure 5-10 gives, as a function of time t, the force component $F_x$ that acts on a 3.00 kg ice block that can move only along the x axis. At t = 0, the block is moving in the positive direction of the axis, with a speed of 3.0 m/s. What are its (a) speed and (b) direction of travel at t= 11 s?

Section 5-4 Additional Problems:

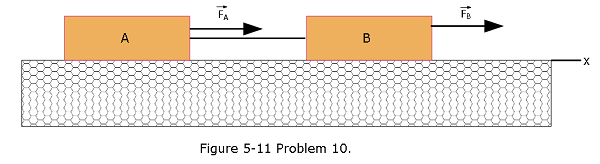
[69] In Fig. 5-11, 4.0 kg block A and 6.0 kg block B are connected by a string of negligible mass. Force $\vec F_A=(12~N)\hat i$ acts on block A; force $\vec F_B=(24~N)\hat j$ acts on block B. What is the tension in the string?