Chapter 2 Motion Along a Straight Line:
Learning Objectives:
In this chapter you will basically learn:
\(\bullet\) Learn to consider an object as if it were a (point-like) particle and its motion.
\(\bullet\) Learn the object’s position is on x axis and make relationship between a particle’s displacement and its initial and final positions, relationship between a particle’s average velocity, its displacement, and the time interval for that displacement, its the relationship between a particle’s average speed, the total distance it moves, and the time interval for the motion.
\(\bullet\) Learn how to find average velocity from a graph of a particle’s position versus time.
\(\bullet\) Learn how to calculate the instantaneous velocity given a particle’s position versus time and verify the result graphically.
\(\bullet\) Learn the particle’s average acceleration, instantaneous acceleration and also verify the results graphically.
\(\bullet\) Learn how to apply constant acceleration, to find the equations of motions relating position, displacement, velocity, acceleration, and elapsed time (Table 2-1).
\(\bullet\) Learn how to convert the equations given in Table 2-1 to free flight (whether upward or downward) and if we can neglect the effects of air on its motion, the particle has a constant downward acceleration with a magnitude g that we take to be \(9.8 m/s^2\).
2.1 Position, Displacement:
A change from position \(x_1\) to position \(x_2\) is called a displacement
\[\begin{equation} \Delta x = x_{2}-x_{1} \tag{2.1} \end{equation}\]
where the symbol \(\Delta\), the Greek uppercase delta, represents a change in a quantity, and it means the final value of that quantity minus the initial value.
As an example, if an object moves from \(x_1 = 2\space m\) to \(x_2 = 12\space m\), then the displacement is \(\Delta x = x_{2}-x_{1} = 12\space m - 2\space m = 10\space m\).The positive result indicates that the motion is in the positive direction. If, instead, the particle moves from \(x_1 = 12\space m\) to \(x_2 = 2\space m\), then the displacement is \(\Delta x = x_{2}-x_{1} = 2\space m - 12\space m = -10\space m\).The negative result indicates that the motion is in the negative direction. The results indicate that displacement can be either positive or negative and therefore displacement has both value or magnitude and direction and is called vector. We will not introduce any further discussion on vector and will be introduced in Vectors in Chapter-3.
2.2 Average Velocity and Speed
Average velocity \(v_{avg}\), which is the ratio of the displacement \(\Delta x\) that occurs during a particular time interval \(\Delta t\) to that interval:
\[\begin{equation} v_{avg} = \frac{\Delta x}{\Delta t}=\frac {x_2-x_1}{t_2-t_1} \tag{2.2} \end{equation}\]
The notation means that the position is \(x_1\) at time \(t_1\) and then \(x_2\) at time \(t_2\). SI unit for \(v_{avg}\) is the meter per second (m/s).
In the average velocity the particle’s displacement \(\Delta x\), the average speed involves the total distance covered, independent of direction and can be calculate using the following formula:
\[\begin{equation} s_{avg}=\frac{total\space distance}{\Delta t} \tag{2.3} \end{equation}\]
2.3 Calculation of Average Velocity from Graph
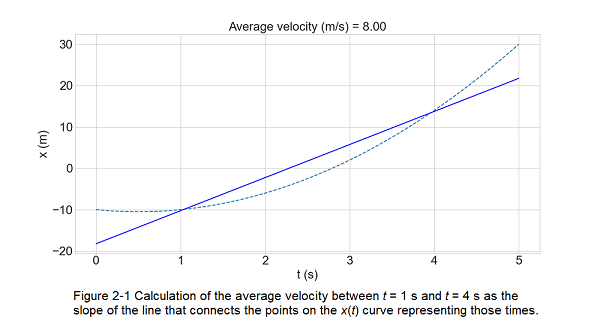
Average velocity \(v_{avg}\)can be calculated using Figure 2-1, for the time interval t = 1.1 s to t = 3.9 s. We draw the straight line that connects the point on the position curve at the beginning of the interval and the point on the curve at the end of the interval.Then we find the slope of the straight line for the given time interval, the average velocity is:
\(v_{avg}= \frac {12.3\space m-(-10.1\space m)}{2.8\space s}= 8\frac{m}{s}\)
2.4 Instantaneous Velocity and Speed
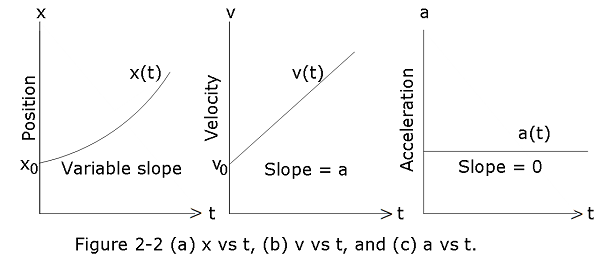
The velocity at any instant is obtained from the average velocity by shrinking the time interval \(\Delta t\) closer and closer to 0. As \(\Delta t\) dwindles, the average velocity approaches a limiting value, which is the velocity at that instant:
\[\begin{equation} v =\displaystyle \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} = \frac{dx}{dt} \tag{2.4} \end{equation}\]
2.5 Acceleration
A motion along an axis, the average acceleration \(a_{avg}\) over a time interval \(\Delta t\) is
\[\begin{equation} a_{avg} =\frac{\Delta v}{\Delta t} = \frac{v_{2}-v_{1}}{t_{2}-t_{1}} \tag{2.5} \end{equation}\]
Instantaneous acceleration (or simply acceleration) a is the first time derivative of velocity v(t) and the second time derivative of position x(t):
\[\begin{equation} a =\displaystyle \lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} = \frac{dv}{dt}= \frac{d^{2}x}{dt^{2}} \tag{2.6} \end{equation}\]
2.6 Constant Acceleration: A Special Case
The average acceleration and instantaneous acceleration are equal when acceleration is constant and we can write Eq. 2-5, with some changes in notation, as
\(a = a_{avg} = \frac{v-v_{0}}{t-0}\)
Here \(v_0\) is the velocity at time t = 0 and v is the velocity at any later time t. We can rewrite this equation as
\[\begin{equation} v = v_{0} + at \tag{2.7} \end{equation}\]
Similarly, manner, we can rewrite Eq. 2-2 (with a few changes in notation) as
\(v_{avg} = \frac{x-x_{0}}{t-0}\)
This equation can be rewritten as
\[\begin{equation} x = x_{0} + v_{avg}t \tag{2.8} \end{equation}\]
in which \(x_{0}\) is the position of the particle at t = 0 and \(v_{avg}\) is the average velocity between t = 0 and a later time t.
For the interval from t = 0 to the later time t then, the average velocity is
\[\begin{equation} v_{avg} = \frac{1}{2}(v + v_{0}) \tag{2.9} \end{equation}\]
Substituting the v from Eq. 2-7 to Eq. 2-9, and after a little rearrangement, we come up with the following equation,
\[\begin{equation} v_{avg} = v_{0} + \frac{1}{2}at \tag{2.10} \end{equation}\]
Substituting \(v_{avg}\) from Eq. 2-10 to Eq. 2-8, we get the second equation of motion,
\[\begin{equation} x - x_{0} = v_{0}t + \frac{1}{2}at^{2} \tag{2.11} \end{equation}\]
We can eliminate the time t between Eqs. 2-7 and 2-11 to produce the third equation of motion in which t does not appear
\[\begin{equation} v^{2} = v_{0}^{2} + 2a(x-x_{0}) \tag{2.12} \end{equation}\]
We can eliminate the acceleration a between Eqs. 2-7 and 2-11 to produce the fourth equation of motion in which a does not appear
\[\begin{equation} x - x_{0} = \frac{1}{2}(v_{0}+v)t \tag{2.13} \end{equation}\]
We can eliminate the \(v_{0}\) between Eqs. 2-7 and 2-11 to produce the fourth equation of motion in which \(v_{0}\) does not appear
\[\begin{equation} x - x_{0} = vt - \frac{1}{2}at^{2} \tag{2.14} \end{equation}\]
Table 2-1 lists the basic constant acceleration equations (Eqs. 2-7 and 2-11) as well as the specialized equations that we have derived.
\(Table~2-1~Equation ~for~ Motion~ with~ Constant~ Acceleration^a\)
| Equation Number | Equation | Missing Quantity |
|---|---|---|
| 2-7 | \(v=v_0+at\) | \(x-x_0\) |
| 2-11 | \(x-x_0=v_0t+\frac{1}{2}at^2\) | v |
| 2-12 | \(v^2=v_0^2+2a(x-x_0)\) | t |
| 2-13 | \(x-x_0=\frac{1}{2}(v_0+v)t\) | a |
| 2-14 | \(x-x_0=vt-\frac{1}{2}at^2\) | \(v_0\) |
Example Problem 2.01 In a highway speed trap, normally two pressure-transducer strips are placed \(120\space m\) apart on a highway on which the speed limit is \(85\space km/h\). A driver going \(110 \space km/h\) suddenly notices a police car just as he/she activates the first strip, and immediately slows down. What deceleration is required so that the car’s average speed is within the speed limit when the car crosses the second strip?
Solution: Let \(v_0= 110 \space {km/h}\) be the speed of the car at the first strip. Let \(\Delta x = 120\space m\) be the distance between the two strips, and let \(\Delta t\) be the time taken by the car to travel from one strip to the other. The average velocity of the car is
\[v_{avg} = \frac{\Delta x}{\Delta t}\] \[\Delta t = \frac{\Delta x}{v_{avg}}=\frac{120\space m}{85\space km/h}\frac{3600\space s/h}{1000\space m/km}=5.08\space s\]
Now, assuming that the acceleration \(a\) of the car is uniform, we have
\[\Delta x = x - x_0=v_0\Delta t+\frac{1}{2}a(\Delta t)^2\] Therefore, \[a= \frac{2(\Delta x-v_0\Delta t)}{(\Delta t)^2}\]
\[a=\frac{2(120\space m-(110\space km/h)({3600\space s/h)}{(1000\space m/km}))(5.08\space s)}{(5.08\space s)^2}= -2.73\space m/s^2\space (Answer)\]
2.7 Free-Fall Acceleration
The equations of motion in Table 2-1 for constant acceleration also apply to free fall near Earth’s surface; that is, they apply to an object in vertical flight, either up or down, when the effects of the air can be neglected. However, note that for free fall: (1) The directions of motion are now along a vertical y axis instead of the x axis, with the positive direction of y upward.(2) The free-fall acceleration is negative—that is, downward on the y axis, toward Earth’s center—and so it has the value -g in the equations.
The acceleration is always a = -g = 9.8 \(\frac{m}{s^2}\), negative and thus downward. The velocity, however, changes, as indicated by Eqs. 2-7 and 2-12: during the ascent, the magnitude of the positive velocity decreases, until it momentarily becomes zero. Adopting these conventions we can come up with a new sets of equations for free-fall acceleration as shown in Table 2-2.
\(Table~2-2~Equation ~for~ Motion~ with~ Constant~ Acceleration^a\)
| Equation Number | Equation | Missing Quantity |
|---|---|---|
| 2-7’ | \(v=v_0-gt\) | \(y-y_0\) |
| 2-11’ | \(y-y_0=v_0t-\frac{1}{2}gt^2\) | v |
| 2-12’ | \(v^2=v_0^2-2g(y-y_0)\) | t |
| 2-13’ | \(y-y_0=\frac{1}{2}(v_0+v)t\) | a |
| 2-14’ | \(y-y_0=vt+\frac{1}{2}gt^2\) | \(v_0\) |
Solved Problems: Motion Along a Straight Line
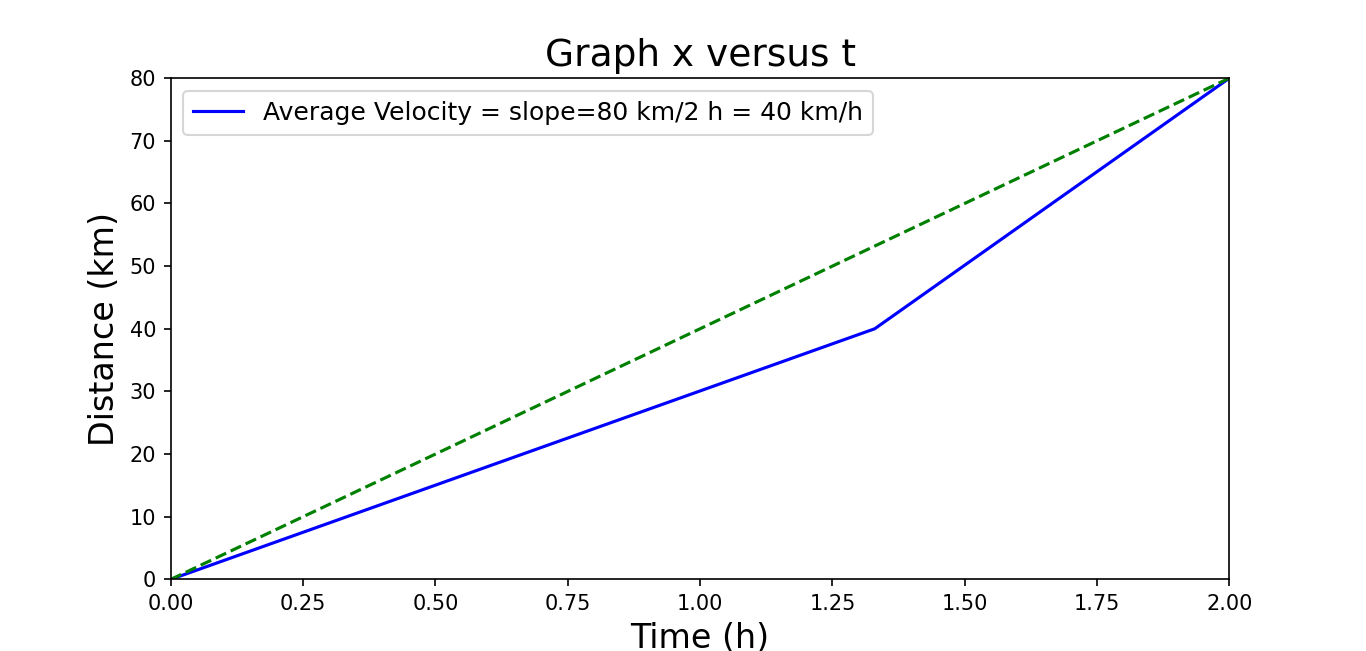
- [3] An automobile travels on a straight road for 40 km at 30 km/h. It then continues in the same direction for another 40 km at 60 km/h. (a) What is the average velocity of the car during the full 80 km trip? (Assume that it moves in the positive x direction.) (b) What is the average speed? (c) Graph x versus t and indicate how the average velocity is found on the graph.
- Time to travel on a straight road for 40 km at 30 km/h: \(t_1 = \frac{40\space km}{30\space km/h}\approx 1.33\space h\)
Time to travel on a straight road for 40 km at 60 km/h: \(t_2 = \frac{40\space km}{60\space km/h}\approx 0.67\space h\)
Total travel time: \(t = t_1 + t_2=1.33~h+0.67~h=2~h\)
\[v_{avg}=\frac{\Delta x}{\Delta t}= v_{avg}=\frac{40\space km+40\space km}{\frac{40\space km}{30\space km/h}+\frac{40\space km}{60\space km/h}}=\frac{80\space km}{2\space h}=+40\space km/h\]
Average speed = \(\frac{total\space distance}{total\space time}=\frac{80~km}{2~h}=40~\frac{km}{h}\)
Graph x versus t and indicate how the average velocity is found on the graph.
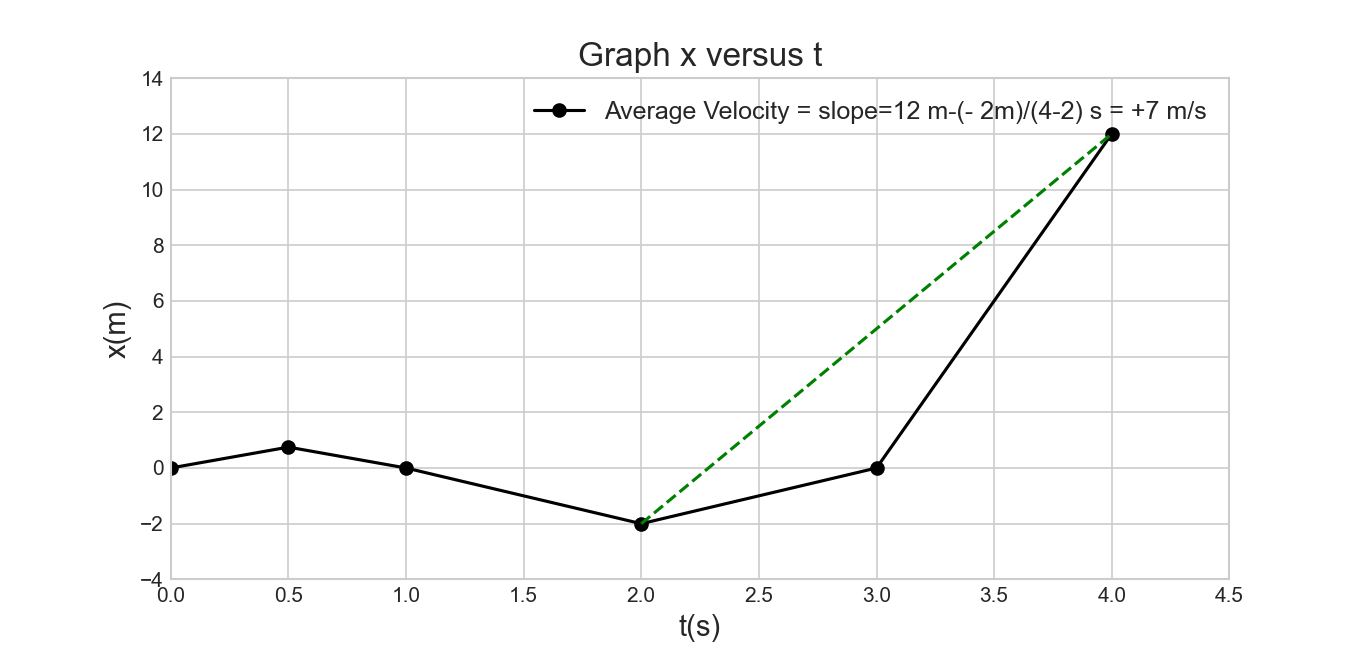
- [5] The position of an object moving along an x axis is given by \(x = 3t - 4t^2+ t^3\), where x is in meters and t in seconds. Find the position of the object at the following values of t: (a) 1 s, (b) 2 s, (c) 3 s, and (d) 4 s. (e) What is the object’s displacement between t = 0 and t = 4 s? (f) What is its average velocity for the time interval from t = 2 s to t = 4 s? (g) Graph x versus t for \(0 \leq t \leq 4 s\) and indicate how the answer for (f) can be found on the graph.
Given \(x(t) = 3t - 4t^2+ t^3\)
- \[x(t=1~s) = 3(1) - 4(1)^2+ (1)^3=0.\]
- \[x(t=2~s) = 3(2) - 4(2)^2+ (2)^3=-2~m.\]
- \[x(t=3~s) = 3(3) - 4(3)^2+ (3)^3=0.\]
- \[x(t=4~s) = 3(4) - 4(4)^2+ (4)^3=12.0~m\]
- Displacement = \[\Delta x = x(t=4~s)-x(t=0)=12.0~m-0=12.0~m\]
- Average Velocity: \[v_{avg}=\frac{\Delta x}{\Delta t}=\frac{x(t=4~s)-x(t=2~s)}{4~s-2~s}=\frac{12~m-(-2~m)}{2~s}=+7~m/s\]
- Graph of x versus t indicating the answer for (f) from the slope of the graph.
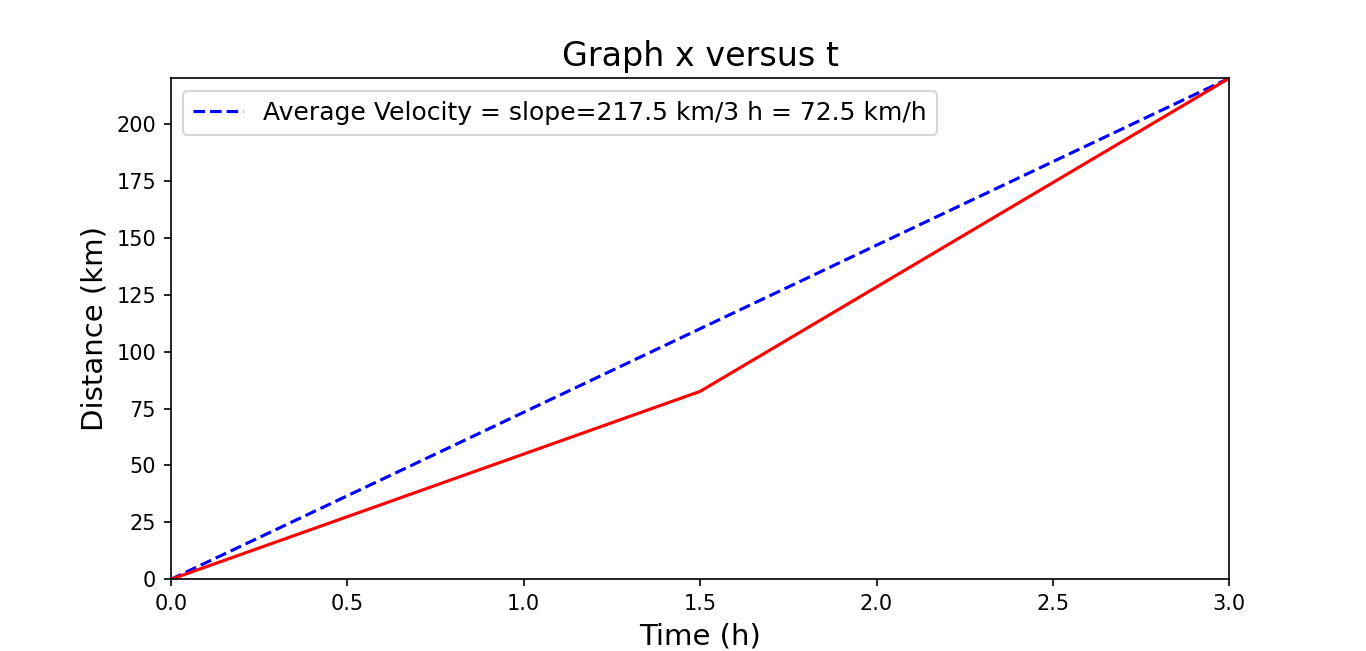
- [13] You drive on Interstate 10 from San Antonio to Houston, half the time at 55 km/h and the other half at 90 km/h. On the way back you travel half the distance at 55 km/h and the other half at 90 km/h. What is your average speed (a) from San Antonio to Houston, (b) from Houston back to San Antonio, and (c) for the entire trip? (d) What is your average velocity for the entire trip? (e) Sketch x versus t for (a), assuming the motion is all in the positive x direction. Indicate how the average velocity can be found on the sketch.
Average speed from San Antonio to Houston: \[S_{avg}=\frac{(55~km/h)(t/2)+(90~km/h)(t/2)}{t}=72.5~km/h\]
Average speed from Houston to San Antonio: \[S_{avg}=\frac{d}{\frac{(d/2)}{(55~km/h)}+\frac{(d/2)}{(90~km/h)}}=68.27~km/h\]
Average speed for the entire trip: \[S_{avg}=\frac{2d}{\frac{(d)}{(72.5~km/h)}+\frac{(d)}{(68.27~km/h)}}=70.3~km/h\]
Average velocity for the entire trip: \[v_{avg}=\frac{Delta x}{\Delta t}=\frac{x_1-x_1}{\Delta t}=0\]
Sketch x versus t for (a), assuming the motion is all in the positive x direction. Assuming the total time for the one way trip is 3 h.
Half of the time i.e., (1.5 h)(55 km/h) = 82.5 km Half of the time i.e., (1.5 h)(90 km/h) = 135.0 km
- [15] (a) If a particle’s position is given by \(x = 4- 12t + 3t^2\) (where t is in seconds and x is in meters), what is its velocity at t = 1 s? (b) Is it moving in the positive or negative direction of x just then? (c) What is its speed just then? (d) Is the speed increasing or decreasing just then? (Try answering the next two questions without further calculation.) (e) Is there ever an instant when the velocity is zero? If so, give the time t; if not, answer no. (f) Is there a time after t = 3 s when the particle is moving in the negative direction of x? If so, give the time t; if not, answer no.
- Velocity of the particle at t = 1 s can be found by differentiating the given equation, i.e.,
\[v (t)=\frac{dx}{dt}=-12 + 6t\] \[v (t=\space 1\space s)=\frac{dx}{dt}=-12 + 6(1\space s)=-6\space m/s.\]
Negative velocity indicates that the particle is moving in the negative x direction.
\(|v(t=1\space s)|=|-6\space m/s|=6\space m/s\)
The speed of the particle is decreasing to zero. \[|v(t=0\space s)|=|-12+(6)(0)|=12\space m/s\] \[|v(t=1\space s)|=|-12+6\times 1|= 6\space m/s\] \[|v(t=2\space s)|=|-12 + 6\times 2|=0\space m/s\]
Velocity is zero at t = 2 s.
Velocity at t = 3s, \(|v(t=3\space s)|=|-12 + 6\times 3|=6\space m/s.\) So, there is no time after t = 3s, that the particle moves in the negative direction of x.
- [34] In Fig. 2-3, a red car and a green car, identical except for the color, move toward each other in adjacent lanes and parallel to an x axis. At time t = 0, the red car is at \(x_r = 0\) and the green car is at \(x_g = 220 m\). If the red car has a constant velocity of 20 km/h, the cars pass each other at x = 44.5 m, and if it has a constant velocity of 40 km/h, they pass each other at x = 76.6 m. What are (a) the initial velocity and (b) the constant acceleration of the green car?
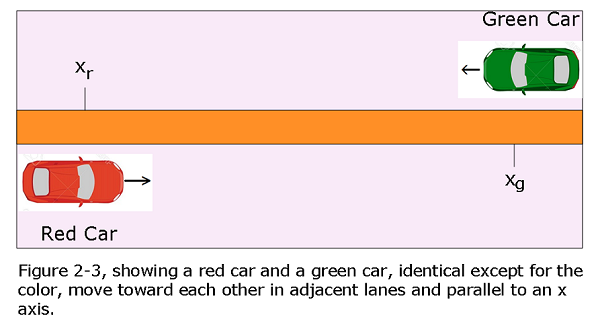
- Given red car’s constant velocity of 20 km/h = 5.55 m/s and 40 km/h = 11.11 m/s.
Red car moves 44.5 m in a time: \(t_1=\frac{44.5\space m}{5.55\space m/s}=8~s\) Red car moves 76.6 m in a time: \(t_2=\frac{76.6\space m}{5.55\space m/s}=6.89~s\)
Green car moves from the other side and meet the red car as follows:
\[44.5-220=v_g(8)+\frac{1}{2}a_g(8)^2~~~~~~~~~~~~~~(1)\] \[76.6-220=v_g(6.89)+\frac{1}{2}a_g(6.89)^2~~~~~~(2)\]
Solving Eqs. (1) and (2) simultaneously, we get the initial velocity of the green car to be v = -13.83 m/s (Answer).
- Solving Eqs. (1) and (2) simultaneously, we get the constant acceleration of the green car to be a = -2.03 \(m/s^2\) (Answer).
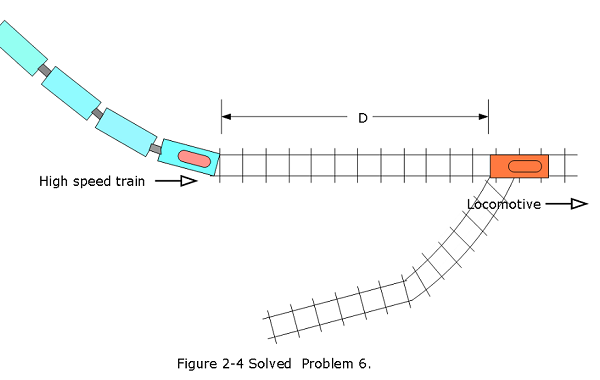
- [43] When a high-speed passenger train traveling at 161 km/h rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance D = 676 m ahead (Fig. 2-4). The locomotive is moving at 29.0 km/h. The engineer of the high-speed train immediately applies the brakes. (a) What must be the magnitude of the resulting constant deceleration if a collision is to be just avoided? (b) Assume that the engineer is at x = 0 when, at t = 0, he first spots the locomotive. Sketch x(t) curves for the locomotive and high-speed train for the cases in which a collision is just avoided and is not quite avoided.
Solution:
(a)Given the high speed train moving at \[v_0 = 161\space \frac{km}{h} = 44.7\space m/s\] and a locomotive moving at \[v = 29\space \frac{km}{h}=8.05\space m/s.\]
Using Eq. 2-13 \[x-x_0 = \frac{1}{2}(v_0+v)t\] \[D + vt -0 = \frac{1}{2}(v_0+v)t\space\] we can find when the high speed train and locomotive will meet each other at time \[\space t = \frac{2D}{v_0-v}=\frac{2(676\space m)}{(44.7-8.05)m/s}=36.8\space s\]
Using Eq. 2-12 \[v^2=v_0^2 + 2a(x-x_0)\] the resulting constant deceleration can be found \[a = \frac{v^2-v_0^2}{2(x-x_0)}=\frac{(8.0\space m/s)^2-(44.7\space m/s)^2}{2(676\space m+vt)}=\frac{(8.0\space m/s)^2-(44.7\space m/s)^2}{2(676\space m+(8.05\space m/s)(36.8\space s))}\] \[a =-0.994\space m/s^2 \space (Answer)\]
- Sketch of x(t) versus t for the locomotive and high-speed train just to avoid collision.
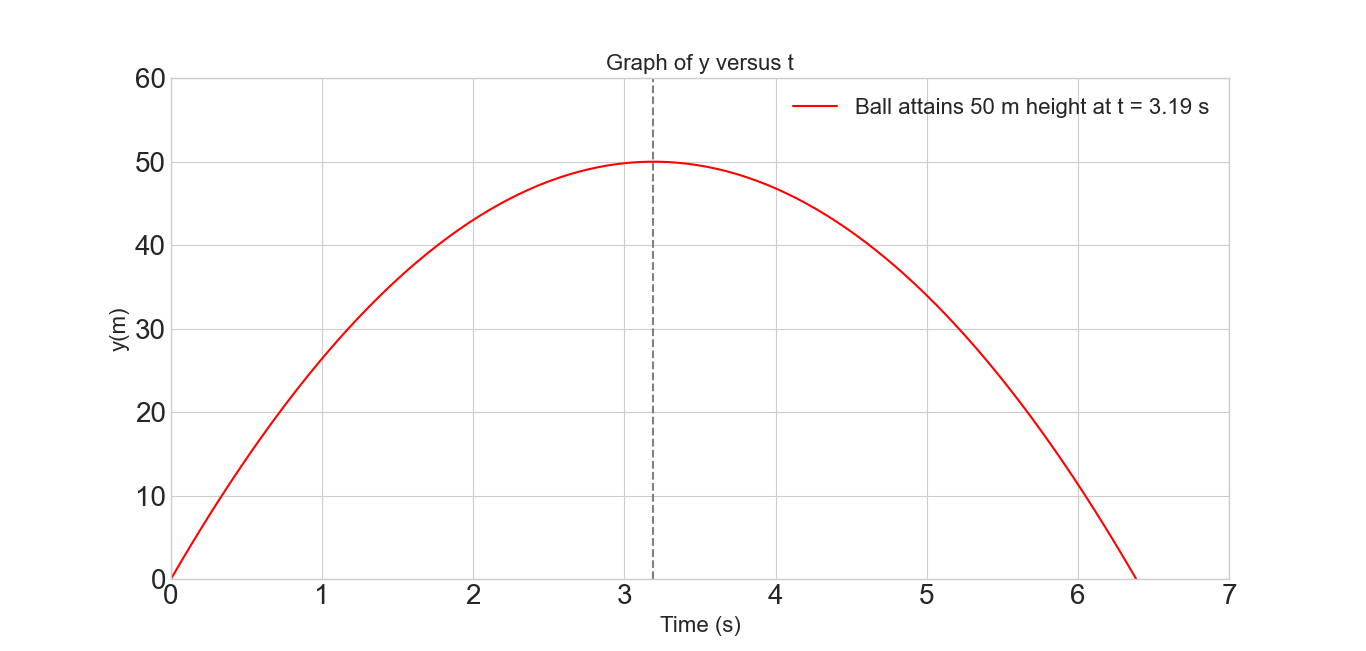
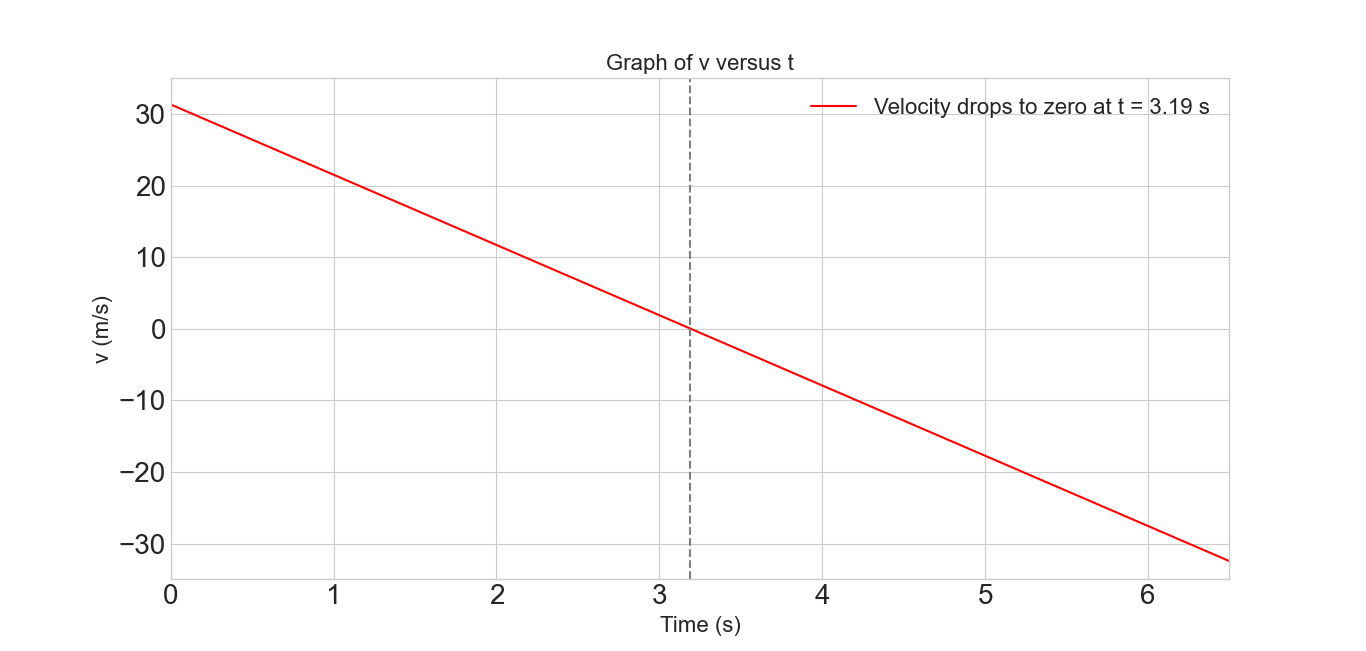
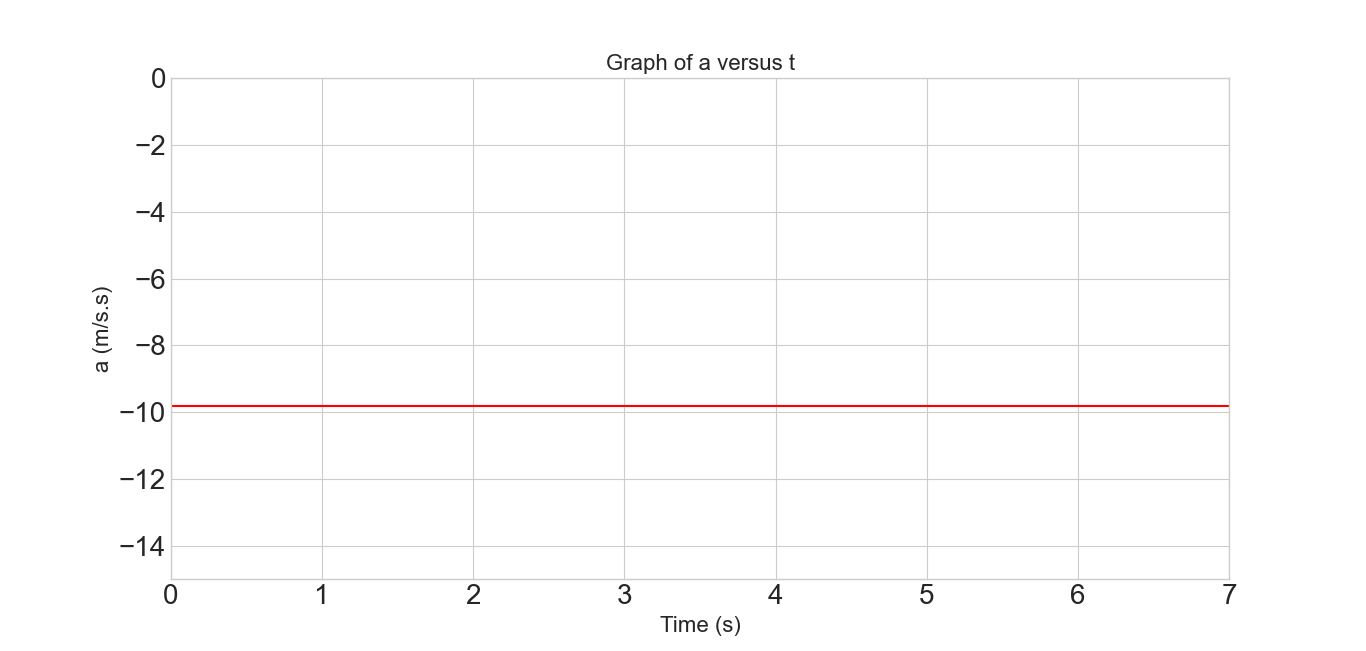
- [45] (a) With what speed must a ball be thrown vertically from ground level to rise to a maximum height of 50 m? (b) How long will it be in the air? (c) Sketch graphs of y, v, and a versus t for the ball. On the first two graphs, indicate the time at which 50 m is reached.
- Using Eq. 2-12’ we can find the initial speed of the ball at a height of 50 m, where final velocity v = 0.
\[v^2=v_0^2-2g(y-y_0)\] \[v_0=\sqrt {2g(y-y_0)}=\sqrt{2\times (9.81~m/s^2)\times (50~m)}=31.32~m/s\]
- Time of flight of the ball is the up and down time together. That is,
\[Total\space time = t_{up}+t_{down}= 2(\frac{v_0}{g})=2\left(\frac{31.32~m/s}{9.81~m/s^2}\right)=6.385~s\approx 6.39~s\]
- Sketch graphs of y, v, and a versus t for the ball.
Problems:Motion Along a Straight Line
Section 2-1 Position, Displacement, and Average Velocity
[2] Compute your average velocity in the following two cases:(a) You walk 73.2 m at a speed of 1.22 m/s and then run 73.2 m at a speed of 3.05 m/s along a straight track. (b) You walk for 1.00 min at a speed of 1.22 m/s and then run for 1.00 min at 3.05 m/s along a straight track. (c) Graph x versus t for both cases and indicate how the average velocity is found on the graph.
[11] You are to drive 300 km to an interview. The interview isat 11:15 A.M. You plan to drive at 100 km/h, so you leave at 8:00 A.M. to allow some extra time.You drive at that speed for the first 100 km, but then construction work forces you to slow to 40 km/h for 40 km.What would be the least speed needed for the rest of the trip to arrive in time for the interview?
Section 2-2 Instantaneous Velocity and Speed
- [17] The position of a particle moving along the x axis is given in centimeters by \(x = 9.75 + 1.50t^3\), where t is in seconds. Calculate (a) the average velocity during the time interval t = 2.00 s to t = 3.00 s; (b) the instantaneous velocity at t = 2.00 s; (c) the instantaneous velocity at t = 3.00 s; (d) the instantaneous velocity at t = 2.50 s; and (e) the instantaneous velocity when the particle is midway between its positions at t = 2.00 s and t = 3.00 s. (f) Graph x versus t and indicate your answers graphically.
Section 2-3 Acceleration
[18] The position of a particle moving along an x axis is given by \(x = 12t^2 - 2t^3\), where x is in meters and t is in seconds. Determine (a) the position, (b) the velocity, and (c) the acceleration of the particle at t = 3.0 s. (d) What is the maximum positive coordinate reached by the particle and (e) at what time is it reached? (f) What is the maximum positive velocity reached by the particle and (g) at what time is it reached? (h) What is the acceleration of the particle at the instant the particle is not moving (other than at t = 0)? (i) Determine the average velocity of the particle between t= 0 and t = 3 s.
[21] From t = 0 to t = 5.00 min, a man stands still, and from t = 5.00 min to t = 10.0 min, he walks briskly in a straight line at a constant speed of 2.20 m/s. What are (a) his average velocity vavg and (b) his average acceleration aavg in the time interval 2.00 min to 8.00 min? What are (c) vavg and (d) aavg in the time interval 3.00 min to 9.00 min? (e) Sketch x versus t and v versus t, and indicate how the answers to (a) through (d) can be obtained from the graphs.
Section 2-4 Constant Acceleration
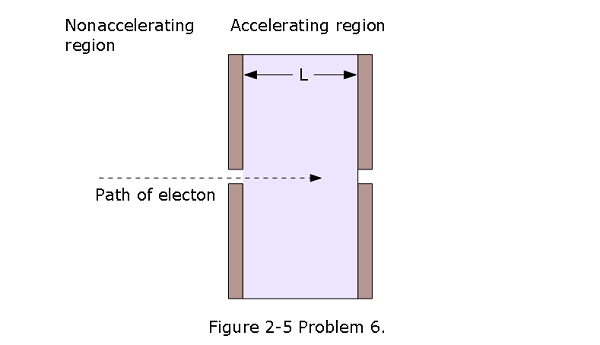
- [23] An electron with an initial velocity \(v_0 = 1.50 \times 10^5~ m/s\) enters a region of length L = 1.00 cm where it is electrically accelerated (Fig. 2-5). It emerges with \(v = 5.70 \times 10^6~ m/s\). What is its acceleration, assumed constant?
[26] A muon (an elementary particle) enters a region with a speed of \(5.00 \times 10^6 ~m/s\) and then is slowed at the rate of \(1.25 \times 10^{14} m/s^2\). (a) How far does the muon take to stop? (b) Graph x versus t and v versus t for the muon.
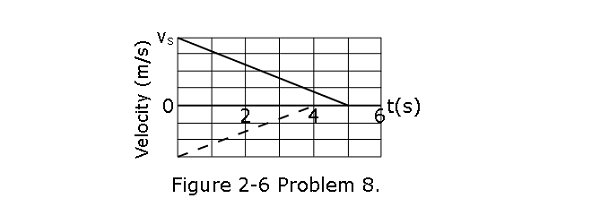
[41] As two trains move along a track, their conductors suddenly notice that they are headed toward each other. Figure 2-6 gives their velocities v as functions of time t as the conductors slow the trains. The figure’s vertical scaling is set by \(v_s = 40.0 m/s\). The slowing processes begin when the trains are 200 m apart.What is their separation when both trains have stopped?
Section 2-5 Free-Fall Acceleration
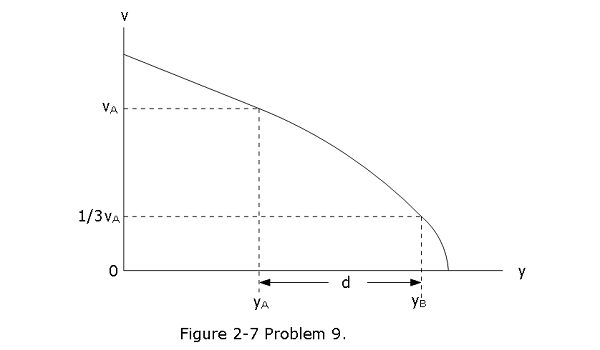
- [56] Figure 2-7 shows the speed v versus height y of a ball tossed directly upward, along a y axis. Distance d is 0.40 m. The speed at height \(y_A\) is \(v_A\).The speed at height \(y_B\) is \(v_A\). What is speed \(v_A\)?
Section 2-6 Graphical Integration in Motion Analysis
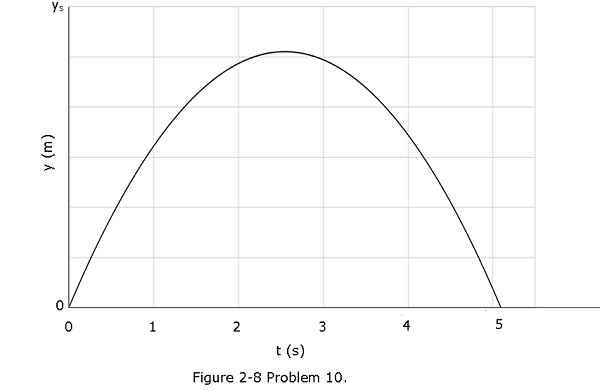
- [64] A ball is shot vertically upward from the surface of another planet. A plot of y versus t for the ball is shown in Fig. 2-8, where y is the height of the ball above its starting point and t = 0 at the instant the ball is shot. The figure’s vertical scaling is set by \(y_s\) = 30.0 m.What are the magnitudes of (a) the free-fall acceleration on the planet and (b) the initial velocity of the ball?