Chapter 6 Force & Motion-II
Learning Objectives:
In this chapter you will basically learn:
\(\bullet\) Learn how to distinguish between static friction and a kinetic friction and how to determine the direction and magnitude of a frictional force.
\(\bullet\) Learn the drag force on an object moving through air, the terminal speed of an object falling through air.
\(\bullet\) Learn what is uniform circular motion and how the velocity, acceleration, and force vectors (magnitudes and directions) are being related during the motion.
6.1 Frictional Force:
Frictional forces help us to walk, car to move and wheel to rotate. Imagine our world is covered with ice or some kind of oily substance on which our normal movements couldn’t be maintained. Although a substantial percent (about 15-20%) of gasoline is used by an automobile or train to overcome the friction but without having friction we couldn’t get around with our our moving devices, we could not walk or ride a bicycle. We are not able hold things with our hands.
An object shows the following properties as it slides from rest to movement upon the application of force:
Property 1. If the object does not move, then the static frictional force \(\vec f_s\) and the applied force \(\vec F\) are parallel to each other with equal magnitude and directed opposite to each other.
Property 2. The magnitude of \(\vec f_s\) has a maximum value \(f{s,max}\) that is given by
\[\begin{equation} f_{s,max} = \mu_sF_N \tag{6.1} \end{equation}\]
where \(\mu_s\) is the coefficient of static friction and \(F_N\) is the magnitude of the normal force on the body from the surface. If the magnitude of the component of \(\vec F\) that is parallel to the surface exceeds \(f_{s,max}\), then the body begins to slide along the surface.
Property 3. Once the object begins to slide along the surface, the magnitude of the frictional force rapidly decreases to a value \(f_k\) and is given by
\[\begin{equation} f_k = \mu_kF_N \tag{6.2} \end{equation}\]
where \(\mu_k\) is the coefficient of kinetic friction.
Example Problem 6.1 Calculate the stopping distances for a car sliding to a stop from an initial speed of 10.0 m/s (36 km/h) on a dry horizontal road, an icy horizontal road, and an icy downhill.
How far does the car slides to a stop on a horizontal road (Fig. 6-1a) if the coefficient of kinetic friction is \(\mu_k = 0.60\)? Assume that the air resistance is negligibly small on the car, and also assume that the wheels of the car are locked up and the wheels slide, along the x-direction of the car’s movement.
What is the stopping distance if the road is covered with ice with \(\mu_k = 0.10\)?
Repeat the calculation assuming that the car sliding down an icy hill with an angle of inclination \(\theta = 5.0^\circ.\)
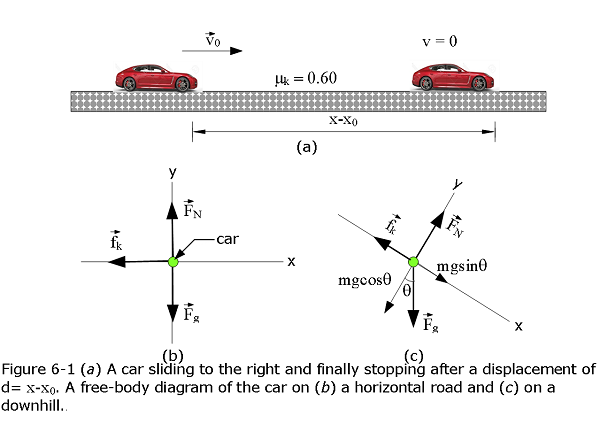
Solution:
- Using free-body diagram of Figure 6-1b, we get
\[\begin{equation} -f_k=ma_x \tag{6.3} \end{equation}\]
Substituting \(f_k = \mu_kF_N\) and \(F_N = mg\) give us
\[\begin{equation} -\mu_kF_N=ma_x \tag{6.4} \end{equation}\]
\[\begin{equation} a_x= -\mu_kg. \tag{6.5} \end{equation}\]
Using Eq. 2-12, \(v^2 = v_0^2+2a(x-x_0)\), we get \(x-x_0=\frac{(v^2-v_0^2)}{2a_x}\)
\[\begin{equation} x-x_0 = \frac{(v^2-v_0^2)}{-2\mu_kg} \tag{6.6} \end{equation}\]
Now substituting v = 0, \(v_0 = 10~m/s\), \(\mu_0=0.60\), and \(g=9.8~m/s^2\), we get \(x-x_0=\frac{(v^2-v_0^2)}{-2\mu_kg}=\frac{(0-(10~m/s)^2)}{-2\times 0.6\times 9.8~m/s}=8.5~m\space(Answer)\)
Changing the value of \(\mu_k = 0.1\) for ice, we get \(x-x_0=\frac{(v^2-v_0^2)}{-2\mu_kg}=\frac{(0-(10~m/s)^2)}{-2\times 0.1\times 9.8~m/s}=51~m.\space(Answer)\)
Resolving the forces along the x and y-components of Figure 6-1c, we get \(-f_k+mg\sin\theta=ma_x\)
\(-\mu_kF_N+mg\sin\theta=ma_x\)
\(F_N=mg\cos\theta\)
\(-mu_k(mg\cos\theta)+mg\sin\theta=ma_x\)
\(a_x=-\mu_kg\cos\theta+g\sin\theta=-(0.10)(9.8~m/s^2)\cos5^\circ+(9.8~m/s^2)\sin5^\circ)=-0.122~m/s^2\)
Using Eq. 6-6, we get
\(x-x_0=\frac{v^2-v_0^2)}{2a_x}=\frac{(0-(10~m/s)^2)}{2(-0.122~m/s^2)}=400~m\space(Answer)\)
Caution!!. This result is a cautionary signal for the drivers. Be careful of driving on the icy roads and highways during winter. In this example the stopping distances 8.5 m, 51 m, and 400 m for a car sliding to a stop from an initial speed of 10.0 m/s (36 km/h) on a dry horizontal road, an icy horizontal road, and an icy downhill respectively. So, the stopping distaces on an icy road is 6 times greater and about 47 times greater than on a slightly inclined road than the dry horizontal road respectively.
6.2 Drag Force & Terminal Speed:
6.3 Uniform Circular Motion:
Solved Problems:Force & Motion-II
- [5] A 2.5 kg block is initially at rest on a horizontal surface. A horizontal force \(\vec F\) of magnitude 6.0 N and a vertical force \(\vec P\) are then applied to the block (Fig. 6-17).The coefficients of friction for the block and surface are \(\mu_s = 0.40\) and \(\mu_k = 0.25\). Determine the magnitude of the frictional force acting on the block if the magnitude of \(\vec P\) is (a) 8.0 N, (b) 10 N, and (c) 12 N.
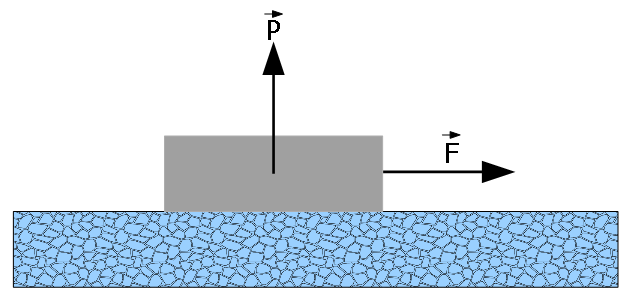
Solution: Applying Newton’s second law: \(\sum\vec F_{net}=m\vec a\)
Components of the forces along the x-axis: \(F-f=ma_x~~~~~~~~~~~~~~~(1)\)
Components of the forces along the y-axis: \(P-F_N-mg=ma_y~~~~~~~~~~(2)\)
where f and \(F_N\) are frictional force and normal force respectively.
- Given \(\vec P=8\space N\), and using Eq. (2) we can calculate \(F_N\)
\(F_N=mg-P=(2.5~kg)(9.8~m/s^2)-8.0~N=16.5~N\)
Now we can calculate the maximum static frictional force: \(f_{s,max}=\mu_sF_N=(0.40)(16.5~N)=6.6~N\)
Since, \(f_{s,max}>F(6.0~N)\), the block doesn’t move, as a result no acceleration.
Using Eq. (1) \(F-f=ma_x(a_x=0).\) Therefore, the frictional force is \(f=F=6.0~N\space(Answer)\)
- Similar to (a), given \(\vec P=10\space N\), and using Eq. (2) we can calculate \(F_N\)
\(F_N=mg-P=(2.5~kg)(9.8~m/s^2)-10.0~N=14.5~N\)
Now we can calculate the maximum static frictional force: \(f_{s,max}=\mu_sF_N=(0.40)(14.5~N)=5.8~N\)
Since, \(f_{s,max}<F(6.0~N)\), the block will move, as a result there is an acceleration.
Using Eq. (1) \(F-f=ma_xa_x\) Therefore, the frictional force is going kinetic \(f_k=\mu_kF_N=(0.25)(14.5~N)=3.625~N\space(Answer)\)
- Similar to (b), given \(\vec P=12\space N\), and using Eq. (2) we can calculate \(F_N\)
\(F_N=mg-P=(2.5~kg)(9.8~m/s^2)-12.0~N=12.5~N\)
Now we can calculate the maximum static frictional force: \(f_{s,max}=\mu_sF_N=(0.40)(12.5~N)=5.0~N\)
Since, \(f_{s,max}<F(6.0~N)\), the block will move, as a result there is an acceleration.
Using Eq. (1) \(F-f=ma_xa_x\) Therefore, the frictional force is going kinetic \(f_k=\mu_kF_N=(0.25)(12.5~N)=3.125~N\space(Answer)\)
- [9] 9 A 3.5 kg block is pushed along a horizontal floor by a force \(\vec F\) of magnitude 15 N at an angle \(\theta=40^\circ\) with the horizontal (Fig. 6-19). The coefficient of kinetic friction between the block and the floor is \(\mu_k = 0.25\). Calculate the magnitudes of (a) the frictional force on the block from the floor and (b) the block’s acceleration.
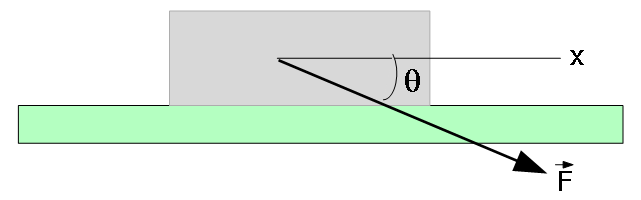
Solution:
Components of the forces along x and y-directions from the Newton’s second law: \(\vec F_{net}=0\)
\[F_N-F_g-F\sin\theta=0~~~~~~~~~~(1)\]
\[-f_k+F\cos\theta = ma~~~~~~~~~~(2)\]
- \(f_k = \mu_kF_N=\mu_k(F\sin\theta+F_g=(0.25)\left[(15~N)\sin40^\circ+(3.5~kg)(9.8~kg/s^2)\right]\)
\(f_k = 10.98\approx 11~N\space(Answer)\)
- Using Eq. 2, the block’s acceleration can be calculated as follows:
\[a = \frac{-f_k+F\cos\theta}{m}=\frac{-11~N+(15~N)\cos40^\circ}{3.5~kg}=0.14~m/s^2\space (Answer)\]
- [13] A worker pushes horizontally on a 35 kg crate with a force of magnitude 110 N.The coefficient of static friction between the crate and the floor is \(\mu_s = 0.37\). (a) What is the value of \(f_{s,max}\) under the circumstances? (b) Does the crate move? (c) What is the frictional force on the crate from the floor? (d) Suppose, next, that a second worker pulls directly upward on the crate to help out. What is the least vertical pull that will allow the first worker’s 110 N push to move the crate? (e) If, instead, the second worker pulls horizontally to help out, what is the least pull that will get the crate moving?
Solution:
Forces acting on the crate can be seen in the following diagram:
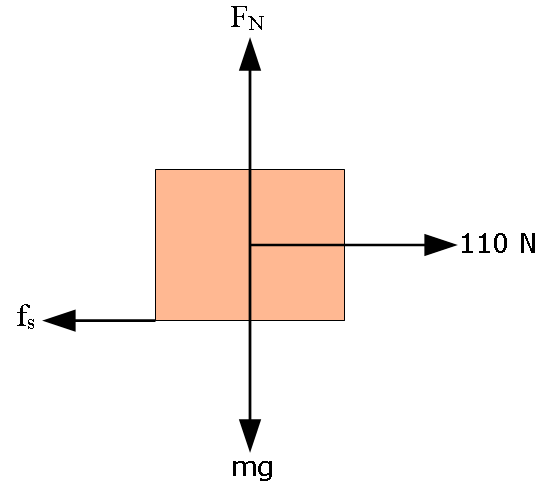
\(f_{s,max}=\mu_sF_N=\mu_smg=(0.37)(35~kg)(9.8~m/s^2)=126.91~N\approx1.3\times10^2~N\space(Answer)\)
No. (Answer) Crate will not move since f_{s,max}>110~N
\(110~N-f_s=0; f_s=110~N=1.1\times10^2~N\space(Answer)\)
\[F_N+F-mg=0\] \[F=mg-F_N=mg-\frac{f_s}{\mu_s}=(35~kg)(9.8~m/s^2)-\frac{110~N}{0.37}=45.70\approx 46~N\space(Answer)\]
Least pull will be required to move the crate is: \(f_{s,max}-f_s=126.91~N-110~N=16.91~N\approx17~N\space(Answer)\)
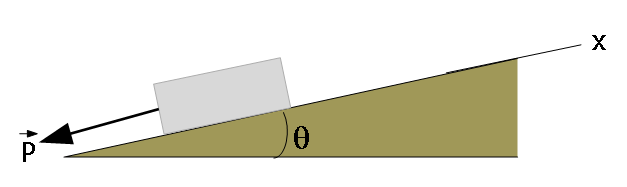
- [17] In Fig. 6-24, a force acts on a block weighing 45 N.The block is initially at rest on a plane inclined at angle \(\theta = 15^\circ\) to the horizontal. The positive direction of the x axis is up the plane. Between block and plane, the coefficient of static friction is \(\mu_s = 0.50\) and the coefficient of kinetic friction is \(\mu_k = 0.34\). In unit-vector notation, what is the frictional force on the block from the plane when \(\vec P\) is (a) \((-5.0 N)\hat i\) , (b) \((-8.0 N)\hat i\) , and (c) \((-15 N)\hat i\) ?
Solution:
Given \(F_g=mg=45~ N\), \(\theta = 15^\circ\), and \(\mu_s=0.50, \mu_k=0.34\)
Let’s show all the forces that are acting on the block as shown in the figure below: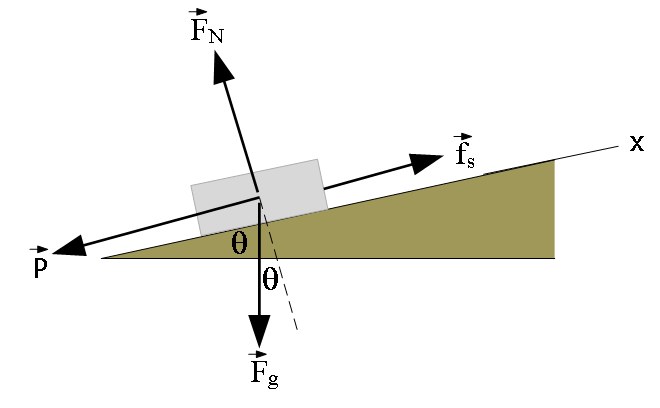
Applying Newton’s second law and resolving the forces along the x-axis and y-axis we get:
\[\vec F_{net}=m\vec a\] \[F_{net,x}=ma_x\] \[f_s-P-F_g\sin\theta=m(0)\] \[f_s=P+F_g\sin\theta~~~~~~~~(1)\], block is at rest \[F_{net,y}=ma_y\] \[F_N-mg\cos\theta=m(0)\] \[F_N=mg\cos\theta~~~~~~~~~~(2)\]
- Given \(|\vec P|=|-5.0~N|=5.0~N\), \(f_s=P+F_g\sin\theta=5.0~N+(45~N)sin45^\circ=16.65~N\)
\(f_{s,max}=\mu_sF_N=\mu_s(mg\cos\theta)=(0.50)(45~N)\cos15^\circ\)
Since, \(f_s < f_{s,max}\), the result is \(f_s\approx 17~N\space(Answer)\)
- Given \(|\vec P|=|-8.0~N|=8.0~N\), \(f_s=P+F_g\sin\theta=8.0~N+(45~N)sin45^\circ=19.65~N<f_{s,max},\)
the result is \(f_s\approx 19.6~N\approx 20~N\space(Answer)\)
- Given \(|\vec P|=|-15.0~N|=15.0~N\), \(f_s=P+F_g\sin\theta=15.0~N+(45~N)sin45^\circ=26.65~N>f_{s,max}\), the block moves
the result is \(f_k=\mu_kF_N=(0.34)(45~N)\cos15^\circ=14.78~N\approx 15~N downward\space(Answer)\)
- [36] The terminal speed of a sky diver is 160 km/h in the spreadeagle position and 310 km/h in the nosedive position. Assuming that the diver’s drag coefficient C does not change from one position to the other, find the ratio of the effective cross-sectional area A in the slower position to that in the faster position.
Solution: \(V_{t,s}=160~km/h=\frac{160\times 10^3~m}{3600~s}=44.44~m/s\)
\(V_{t,n}=310~km/h=\frac{310\times 10^3~m}{3600~s}=86.11~m/s\)
\(\left(\frac {V_{t,s}}{V_{t,n}}\right)^2=\left(\frac{2F_g}{C\rho A_S}\right)/\left(\frac{2F_g}{C\rho A_n}\right)\)
\(\frac{A_s}{A_n}=\left(\frac{V_{t,s}}{V_{t,n}}\right)^2=\left(\frac{86.11~m/s}{44.44~m/s}\right)^2=3.75\)
- [39] Calculate the ratio of the drag force on a jet flying at 1000 km/h at an altitude of 10 km to the drag force on a propdriven transport flying at half that speed and altitude. The density of air is 0.38 \(kg/m^3\) at 10 km and 0.67 \(kg/m^3\) at 5.0 km. Assume that the airplanes have the same effective cross-sectional area and drag coefficient C.
Solution:
\(\frac{D_{10}}{D_5}=\frac{(1/2)C\rho_{10} A V_{10}^2}{(1/2)C\rho_5 A V_{10}^2}=\frac{\rho_{10}V_{10}^2}{\rho_{5}V_{5}^2}\)
\(\frac{D_{10}}{D_5}=\frac{\rho_{10}V_{10}^2}{\rho_{5}V_{5}^2}=\frac{(0.38~kg/m^3)(1000~km/h)^2}{(0.67~kg/m^3)(500~km/h)^2}=2.27\)
- [43] What is the smallest radius of an unbanked (flat) track around which a bicyclist can travel if her speed is 29 km/h and the ms between tires and track is 0.32?
Solution:
\(\mu_sF_N=m(\frac{V^2}{R})\)
\(R=\frac{V^2}{\mu_sg}=\frac{\left(\frac{29\times 10^3~m}{3600~s}\right)^2}{(0.32)(9.8~m/s^2)}=20.69\approx 21~m~(Answer)\)
- [45] A student of weight 667 N rides a steadily rotating Ferris wheel (the student sits upright). At the highest point, the magnitude of the normal force \(\vec F_N\) on the student from the seat is 556 N. (a) Does the student feel “light” or “heavy” there? (b) What is the magnitude of \(\vec F_N\) at the lowest point? If the wheel’s speed is doubled, what is the magnitude \(F_N\) at the (c) highest and (d) lowest point?
Solution:
- At the top \(F_{N,top}-F_g=-\frac{mv^2}{r}\) \(556~N-667~N=-f_c\)
\(f_c=111~N\), so the student feels lighter.
\(F_N-F_g=f_c\), \(F_N=F_g+f_c=667~N+111~N=778~N\space(Answer)\)
If v is doubled, \(f_c'=\frac{m(2v)^2}{r}=4(f_C)=4(111~N)=444~N\)
At the top, \(F_{N,top}=F_g-f_c'=667~N-444~N=223~N\)
- At the bottom, \(F_{N,bot}=F_g+f_c'=667~N+444~N=1111~N\)
Problems:Force & Motion-II
Section 6-1 Friction:
[6] A baseball player with mass m = 79 kg, sliding into second base, is retarded by a frictional force of magnitude 470 N.What is the coefficient of kinetic friction mk between the player and the ground?
[10] Figure 6-20 shows an initially stationary block of mass m on a floor. A force of magnitude 0.500mg is then applied at upward angle \(\theta=20^\circ\). What is the magnitude of the acceleration of the block across the floor if the friction coefficients are (a) \(\mu_s = 0.600\) and \(\mu_k = 0.500\) and (b) \(\mu_s = 0.400\) and \(\mu_k = 0.300\)?
- [19] A 12 N horizontal force pushes a block weighing 5.0 N against a vertical wall (Fig. 6-26). The coefficient of static friction between the wall and the block is \(\mu_s=0.60\), and the coefficient of kinetic friction is \(\mu_k=0.40\). Assume that the block is not moving initially. (a) Will the block move? (b) In unit-vector notation, what is the force on the block from the wall?
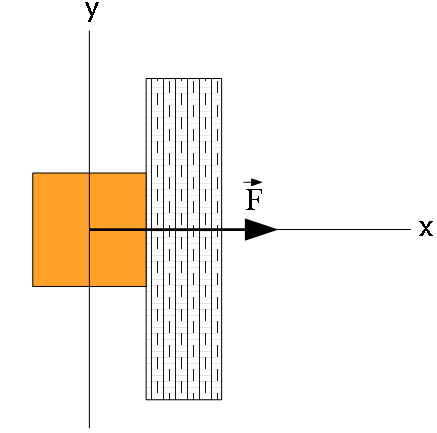
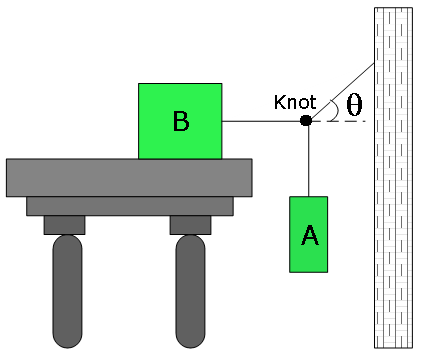
- [25] Block B in Fig. 6-31 weighs 711 N.The coefficient of static friction between block and table is 0.25; angle u is 303; assume that the cord between B and the knot is horizontal. Find the maximum weight of block A for which the system will be stationary.
Section 6-2 The Drag Force and Terminal Speed:
- [38] Assume Eq. 6-14 gives the drag force on a pilot plus ejection seat just after they are ejected from a plane traveling horizontally at 1300 km/h. Assume also that the mass of the seat is equal to the mass of the pilot and that the drag coefficient is that of a sky diver. Making a reasonable guess of the pilot’s mass and using the appropriate \(v_t\) value from Table 6-1, estimate the magnitudes of
- the drag force on the pilot + seat and (b) their horizontal deceleration (in terms of g), both just after ejection. (The result of (a) should indicate an engineering requirement:The seat must include a protective barrier to deflect the initial wind blast away from the pilot’s head.)
- [40] In downhill speed skiing a skier is retarded by both the air drag force on the body and the kinetic frictional force on the skis. (a) Suppose the slope angle is \(\theta = 40.0^\circ\), the snow is dry snow with a coefficient of kinetic friction \(\mu_k = 0.0400\), the mass of the skier and equipment is m = 85.0 kg, the cross-sectional area of the (tucked) skier is \(A = 1.30 m^2\), the drag coefficient is C = 0.150, and the air density is \(1.20 kg/m^3\). (a) What is the terminal speed? (b) If a skier can vary C by a slight amount dC by adjusting, say, the hand positions, what is the corresponding variation in the terminal speed?
Section 6-3 Uniform Circular Motion:
[42] Suppose the coefficient of static friction between the road and the tires on a car is 0.60 and the car has no negative lift. What speed will put the car on the verge of sliding as it rounds a level curve of 30.5 m radius?
[46] A police officer in hot pursuit drives her car through a circular turn of radius 300 m with a constant speed of 80.0 km/h. Her mass is 55.0 kg.What are (a) the magnitude and (b) the angle (relative to vertical) of the net force of the officer on the car seat? (Hint: Consider both horizontal and vertical forces.)
[49] In Fig. 6-39, a car is driven at constant speed over a circular hill and then into a circular valley with the same radius. At the top of the hill, the normal force on the driver from the car seat is 0. The driver’s mass is 70.0 kg.What is the magnitude of the normal force on the driver from the seat when the car passes through the bottom of the valley?

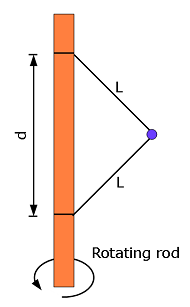
- [59] In Fig. 6-45, a 1.34 kg ball is connected by means of two massless strings, each of length L = 1.70 m, to a vertical, rotating rod.The strings are tied to the rod with separation d = 1.70 m and are taut.The tension in the upper string is 35 N. What are the (a) tension in the lower string, (b) magnitude of the net force on the ball, and (c) speed of the ball? (d) What is the direction of \(F_{net}\)?
Additional Problems:
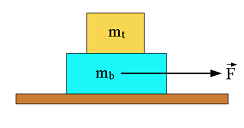
- [61] A block of mass \(m_t = 4.0 kg\) is put on top of a block of mass \(m_b = 5.0 kg\).To cause the top block to slip on the bottom one while the bottom one is held fixed, a horizontal force of at least 12 N must be applied to the top block.The assembly of blocks is now placed on a horizontal, frictionless table (Fig. 6-47). Find the magnitudes of (a) the maximum horizontal force that can be applied to the lower block so that the blocks will move together and (b) the resulting acceleration of the blocks.
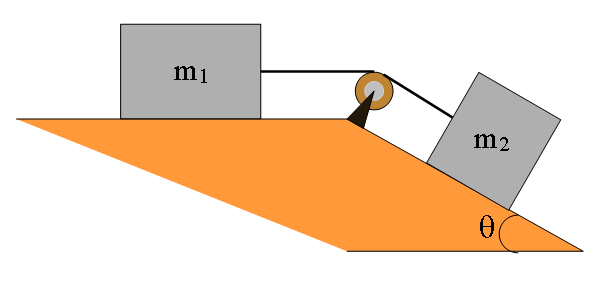
- [66] In Fig. 6-50, block 1 of mass \(m_1 = 2.0 ~kg\) and block 2 of mass \(m_2 = 3.0 ~kg\) are connected by a string of negligible mass and are initially held in place. Block 2 is on a frictionless surface tilted at \(\theta = 30^\circ\)$. The coefficient of kinetic friction between block 1 and the horizontal surface is 0.25. The pulley has negligible mass and friction. Once they are released, the blocks move. What then is the tension in the string?