Chapter 13 Gravitation:

Learning Objectives:

In this chapter you will basically learn:

\(\bullet\) Apply Newton’s law of gravitation to relate the gravitational force between two particles to their masses and their separation.

\(\bullet\) Distinguish between the free-fall acceleration and the gravitational acceleration.

\(\bullet\) Calculate the gravitational acceleration near but outside a uniform, spherical astronomical body.

\(\bullet\) Distinguish between measured weight and the magnitude of the gravitational force.

\(\bullet\) Calculate the gravitational potential energy of a system of particles (or uniform spheres that can be treated as particles).

\(\bullet\) Identify that if a particle moves from an initial point to a final point while experiencing a gravitational force, the work done by that force (and thus the change in gravitational potential energy) is independent of which path is taken.

\(\bullet\) Apply the conservation of mechanical energy (including gravitational potential energy) to a particle moving relative to an astronomical body (or some second body that is fixed in place).

\(\bullet\) Explain the energy requirements for a particle to escape from an astronomical body (usually assumed to be a uniform sphere).

\(\bullet\) Calculate the escape speed of a particle in leaving an astronomical body.

\(\bullet\) Kepler’s three laws of planetary motion.

\(\bullet\) On a sketch of an elliptical orbit, identify the semimajor axis, the eccentricity, the perihelion, the aphelion, and the focal points.

\(\bullet\) For an elliptical orbit, apply the relationships between the semimajor axis, the eccentricity, the perihelion, and the aphelion.

\(\bullet\) For an orbiting natural or artificial satellite, apply Kepler’s relationship between the orbital period and radius and the mass of the astronomical body being orbited.

\(\bullet\) For a satellite in a circular orbit around an astronomical body, calculate the gravitational potential energy, the kinetic energy, and the total energy.

\(\bullet\) For a satellite in an elliptical orbit, calculate the total energy.

\(\bullet\) Explain Einstein’s principle of equivalence.

\(\bullet\) Identify Einstein’s model for gravitation as being due to the curvature of spacetime.

13.0.1 Newtonian Gravity

Newtonian mechanics was initially developed in order to account for the motion of the Planets around the Sun. All matter exerts a force, called gravity, that pulls all other matter towards its center. The strength of the force depends on the mass of the object. The Sun is about 328 times heavier than the Earth and as a result it has more gravity than Earth. As an example Jupiter is 318 times heavier than Earth, and its gravity is \(22.9\space m/s^2\) whereas Earth’s gravity on its surface is \(9.8~m/s^2\). Objects far from the Sun won’t be influenced by its gravity. The force that keeps the Planets in their respective orbits around the Sun is called gravitational force and was first described by Isaac Newton in his Philosophiae Naturalis Principia Mathematica (“Mathematical Principles of Natural Philosophy,”) published in 1687. According to Newton, any two point mass objects (or spherically symmetric objects of finite extent) exert a force of attraction on one another. This force points along the line of centers joining the objects, is directly proportional to the product of their masses, and inversely proportional to the square of the distance between them.

Let’s assume that the first object is the Sun, with mass \(M\), and is located at the origin of our coordinate system. Let’s assume that the second object be a planet, of mass \(m\), which is located at position vector \({\vec r}\). The gravitational force exerted on the planet by the Sun is thus written

\[\begin{equation} \vec F = - \frac{G\,M\,m}{r^3}\,{\vec r}. \tag{13.1} \end{equation}\]

The constant of proportionality, \(G\), is called the universal gravitational constant, and its value in SI unit is given by:

\[\begin{equation} G = 6.67300\times 10^{-11}\space \frac{m^3}{kg-s^2}. \tag{13.2} \end{equation}\]

We shall assume that the Sun is so much more massive than the planet in question that the force exerted by the planet does not cause the Sun’s position to shift appreciably. Hence, the Sun will always remain at the origin of our coordinate system. Likewise, we shall neglect the gravitational forces exerted on our planet by the other planets in the Solar System, compared to the much larger gravitational force exerted by the Sun.

According to Eq. 1, the gravitational force acting on an object is directly proportional to its inertial mass. This question perplexed physicists for many years, and was only answered when Albert Einstein published his general theory of relativity in 1916. According to Einstein, inertial mass acts as a sort of gravitational charge since it is impossible to distinguish an acceleration produced by a gravitational field from an apparent acceleration generated by observing in a non-inertial reference frame. The assumption that these two types of acceleration are indistinguishable leads directly to all of the strange predictions of general relativity such as clocks in different gravitational potentials run at different rates, time-space curvature etc.

Applying Newton’s second law in Eq. 1, the equation of motion of our planet takes the following form

\[\begin{equation} m\frac{d^2{\vec r}}{dt^2} = -\frac{GmM}{r^3}\,{\vec r}. \tag{13.3} \end{equation}\]

\[\begin{equation} \frac{d^2{\vec r}}{dt^2} = -\frac{G\,M}{r^3}\,{\vec r}. \tag{13.4} \end{equation}\]

Note that the planetary mass, \(m\), has canceled out from both sides of the above equation.

13.0.2 Gravitation Near Earth’s Surface:

Assuming Earth is a uniform sphere of mass M. Please don’t get confused with capital M, being the mass of earth now. In the last paragraph we considered M being the mass of Sum and m was the mass of a planet. The magnitude of the gravitational force from Earth on a particle of mass m, located outside Earth at a distance r from Earth’s center, is then given by

\[\begin{equation} {F} = \frac{G\,M\,m}{r^2}\ \tag{13.5} \end{equation}\]

all objects fall toward the center of Earth due to gravitational field around the Earth . The result of gravitational force \(\vec F\) and its associated acceleration we call the gravitational acceleration \(\vec a_g\). Newton’s second law tells us that magnitudes F and \(a_g\) are related by

\[\begin{equation} {F} = ma_g \tag{13.6} \end{equation}\]

\[\begin{equation} a_g = \frac{G\,M}{r^2}\ \tag{13.7} \end{equation}\]

Table 13-1 shows values of \(a_g\) computed for various altitudes above Earth’s surface. Notice that \(a_g\) is significant even at 400 km.

Table 13-1 Variation of \(a_g\) with Altitude

Altitude (km)	\(a_g (m/s^2)\)	Altitude Example
0	9.83	Mean Earth surface
8.8	9.80	Mt. Everest
36.6	9.71	Highest crewed balloon
400	8.70	Space shutte orbit
35700	0.225	Communications satellite

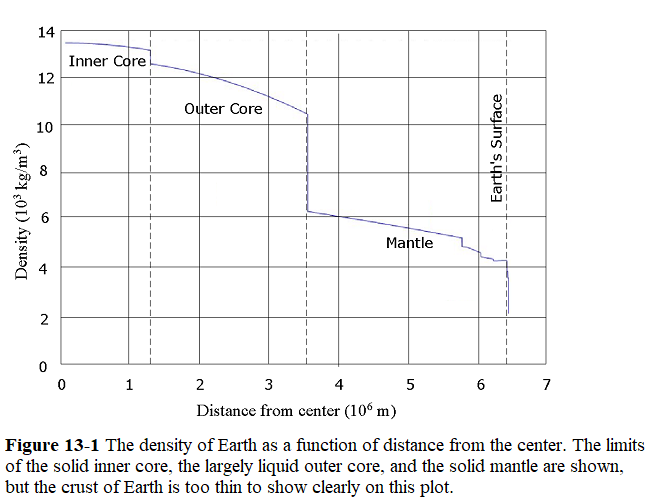
In Chapter 5, of my book on “The Fundamentals of Newtonian Mechanics” we made an assumption that Earth is a non-accelerating inertial frame by neglecting its rotation on its own axis. This assumption led us to assume that the free-fall acceleration \(g\) of a particle is the same as the particle’s gravitational acceleration \(a_g\). Also, we assumed that \(g\) has the constant value \(9.8 ~\frac {m}{s_2}\) any place on Earth’s surface. However, any \(g\) value measured at a given location will differ from the \(a_g\) value calculated with Eq. 13-7 for that location for three reasons: (1) Earth’s mass is not distributed uniformly (Fig. 13-1), (2) Earth is not a perfect sphere, and (3) Earth rotates about its own axis through the poles.

Moreover, because \(g\) differs from \(a_g\), as a result the measured weight \(mg\) of a particle differs from the magnitude of the gravitational force on the particle as given by Eq. 5. Let us now examine those reasons.

1. Non-uniform Distribution of Earth’s Mass. The density (mass per unit volume) of Earth varies radially as shown in Fig. 1, as a result g varies from region to region over the surface.

2. Earth is not a sphere. Earth is slightly ellipsoidal in shape. Its equatorial radius (from its center point out to the equator) is greater by 21 km than its polar radius (from its center point out to either north or south pole). On in other words a point at the poles is closer to the dense core of Earth than is a point on the equator. The free-fall acceleration g slightly more than the equator (see Eq. 13-7).

3. Earth is rotating. Earth is rotating with a period of T = 24 hrs about an axis of rotation passing through the poles. A rotating Earth has maximum centripetal acceleration or a centripetal net force directed toward the Earth’s center at the equator and minimum at the poles.

The effect of rotation on g can be easily calculated by considering a free-body diagram for the crate as shown in Figure 13-2. As can be seen in Figure 13-2, two forces acting on the crate, one is the normal force \(\vec F_N\) directed radially upward and the other one is The gravitational force \(m\vec g\) directed radially towards the center of the Earth.

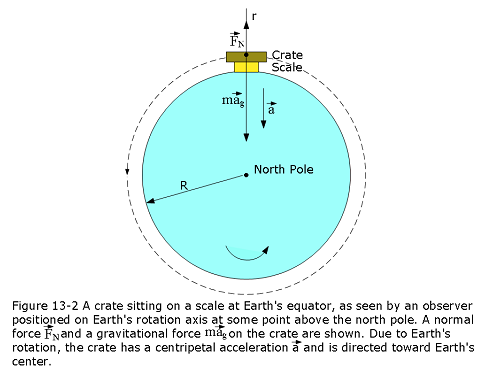
Using Newton’s second law for forces along the radial direction

\[\begin{equation} F_{net,r} = ma_r \tag{13.8} \end{equation}\]

\[\begin{equation} F_N -ma_g = m(-\omega^2R) \tag{13.9} \end{equation}\]

The magnitude \(F_N\) of the normal force is equal to the weight mg read on the scale. Substituting \(F_N = mg\) in Eq. 23-9 gives us

\[\begin{equation} mg = ma_g -m(\omega^2R) \tag{13.10} \end{equation}\]

\[\begin{equation} g = a_g -(\omega^2R) \tag{13.11} \end{equation}\]

where \(\omega=\frac{2\pi}{T}\), with \(T=24~h\) is the period of rotation of Earth on its own axis. The measured free-fall acceleration is less than the gravitational acceleration because the of Earth’s rotation.

Considering \(T=24~h\) and radius of Earth \(R=6.37\times 10^6\space m\), he value of \(\omega^2R=\frac{4pi^2R}{T^2}=0.03369~m/s^2\), and which is small compared to \(g=9.8~m/s^2.\) This little centripetal acceleration at the equator due to Earth’s rotation on its own axis make the Earth slightly non-inertial.

13.0.3 Gravitational Potential Energy:

We want to find the gravitational potential energy U of the base ball at point P along its path, at radial distance R from Earth’s center as shown in Fig. 13-3.

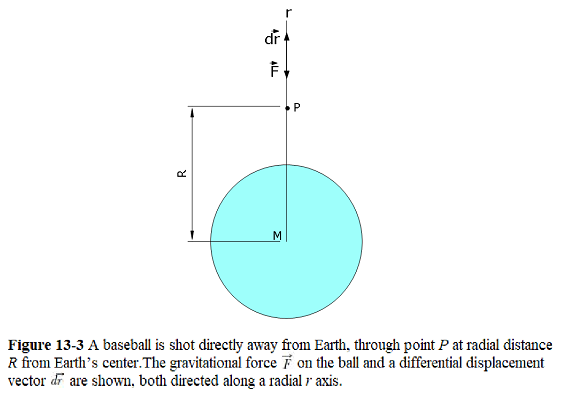
To find the gravitational potential energy U, we first find the work W done on the ball by the gravitational force as the ball travels from point P to a great (infinite) distance from Earth. Because the gravitational force (r) is a variable force (its magnitude depends on r). In vector notation, we can write

\[\begin{equation} W = \int_R^{\infty}\vec F(r).d\vec r = \int_R^{\infty}F(r)dr\cos\phi = \int_R^{\infty}F(r)dr\cos180^0=-\int_R^{\infty}F(r)dr \tag{13.12} \end{equation}\]

substituting Eq. 13-5 in Eq. 13-12, we get the final expression for W, as follows:

\[\begin{equation} W = -\int_R^{\infty}F(r)dr=-{GMm}\int_R^{\infty}\frac{1}{r^2}dr=-\frac{GMm}{R} \tag{13.13} \end{equation}\]

where M is the mass of Earth and m is the mass of the baseball taken into consideration in this example. We know from Eq. 8-1 (\(\Delta U = -W\)) tells us that we can also write that work in terms of potential energies as

\[U_{\infty}-U = -W\] \[U = W=-\frac{GMm}{R},\] where we assumed the gravitational potential engery, \(U_{\infty}=0\), at infinity.

13.0.4 Escape Speed:

If a projectile is thrown upward with a certain minimum initial speed that will cause it to move upward forever, theoretically coming to rest only at infinity. This minimum initial speed is called the (Earth) escape speed.

Applying the principle of conservation of energy, the total energy at the planet’s surface must be zero

\[K+U = \frac{1}{2}mv^2+\left(-\frac{GMm}{R}\right)=0\]

\[\begin{equation} v=\sqrt\frac{2GM}{R} \tag{13.14} \end{equation}\]

Note that v does not depend on the direction in which a projectile is fired from a planet. However, attaining that speed is easier if the projectile is fired in the direction the launch site is moving as the planet rotates about its axis. For example, rockets are launched eastward at Cape Canaveral to take advantage of the Cape’s eastward speed of 1500 km/h due to Earth’s rotation.

Eq. 13-14 can be used to find the escape speeds for various astronomical objects, taking into consideration of the masses M and radii R of the respective objects under consideration. Table 13-2 shows some escape speeds.

Table 13-2 Some Escape Speeds

Body	Mass (kg)	Radius (m)	Escape speed (km/s)
\(Ceres^a\)	\(1.17\times 10^{21}\)	\(3.8\times 10^5\)	0.64
\(Earth's moon^a\)	\(7.36\times 10^{22}\)	\(1.74\times 10^{6}\)	2.38
Earth	\(5.98\times 10^{24}\)	\(6.37\times 10^{6}\)	11.2
Jupiter	\(1.90\times 10^{27}\)	\(7.15\times 10^{7}\)	59.5
Sun	\(1.99\times 10^{30}\)	\(6.96\times 10^{8}\)	618
\(Sirius B^b\)	\(2\times 10^{30}\)	\(1\times 10^{7}\)	5200
\(Neutron star^c\)	\(2\times 10^{30}\)	\(1\times 10^{4}\)	\(2\times 10^5\)

\(^a\) The most massive of the asteroids.

\(^b\) A white dwarf (a star in a final stage of evolution) that is a companion of the bright star Sirius.

\(^c\) The collapsed core of a star that remains after that star has exploded in a supernova event.

13.0.5 Conservative Force:

We have seen the force of gravity is a conservative force in Eq. 5-21. Hence, we can rewrite the gravitational force (13-1) in terms of Eq.5-21

\[\begin{equation} {\vec F} = - \vec \nabla U(\vec r), \tag{13.15} \end{equation}\]

where the potential energy, \(U({\vec r})\), of our planet in the Sun’s gravitational field takes the form

\[\begin{equation} U({\vec r}) = - \frac{G\,M\,m}{r^2}{\vec r}. \tag{13.16} \end{equation}\]

It follows that the total energy of our planet is a conserved or constant quantity. In other words,

\[\begin{equation} {\ E} = {\ K} + {\ U} = \frac{mv^2}{2} - \frac{G\,Mm}{r} \tag{13.17} \end{equation}\]

or in other words, total energy is the sum of kinetic energy (K) and potential energy (U) is constant in time. Here, \({E}\) is the planet’s total energy, and \({\vec v} = d{\vec r}/dt\) is the linear velocity.

Gravity is also a central force and the angular momentum of our planet is a conserved quantity. In other words,

\[\begin{equation} {\vec l} = {\vec r}\times {\vec p}, \tag{13.18} \end{equation}\]

where \(\vec p = m\vec v\) is the linear momentum, \(\vec l\) is the planet’s angular momentum, is constant in time. Taking the scalar product of the above equation with \({\vec r}\), we obtain

\[\begin{equation} {\vec l}\cdot{\vec r} = 0. \tag{13.19} \end{equation}\]

This is the equation of a plane which passes through the origin, and whose normal is parallel to \({\vec l}\). Since \({\vec l}\) is a constant vector, it always points in the same direction. We, therefore, conclude that the motion of our planet is two-dimensional in nature: i.e., it is confined to some fixed plane which passes through the origin. Without loss of generality, we can let this plane coincide with the \(x\)-\(y\) plane.

13.0.6 Polar Coordinate System:

Polar coordinate system is shown in Figure 13-4 with respect to \(x\)-\(y\) cartesian coordinate system. We can determine the instantaneous position of our planet in the \(x\)-\(y\) plane in terms of standard Cartesian coordinates, (\(x\), \(y\)), or polar coordinates, (\(r\), \(\theta\)), as can be seen in Figure 13-4.

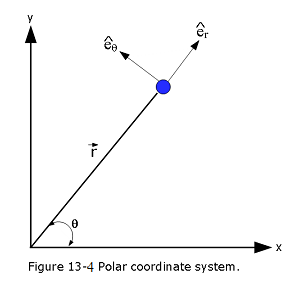
The magnitude of the position vector \(\vec r\) and direction are, \(r=\sqrt{x^2+y^2}\) and \(\theta=\tan^{-1}(y/x)\) respectively. The instantaneous position of the planet can be defined in terms of two unit vectors, \({\hat e}_r\equiv {\hat r}/r\) and \({\hat e}_\theta\equiv {\hat e}_z\times {\hat e}_r\). The position unit vector points radially outward from the origin, whereas the second is normal to the first, in the direction of increasing \(\theta\). The Cartesian components of \({\hat e}_r\) and \({\hat e}_\theta\) are

\[\begin{equation} {\hat e}_r = (\cos\theta,\sin\theta), \tag{13.20} \end{equation}\]

\[\begin{equation} {\hat e}_\theta = (-\sin\theta,\cos\theta). \tag{13.21} \end{equation}\]

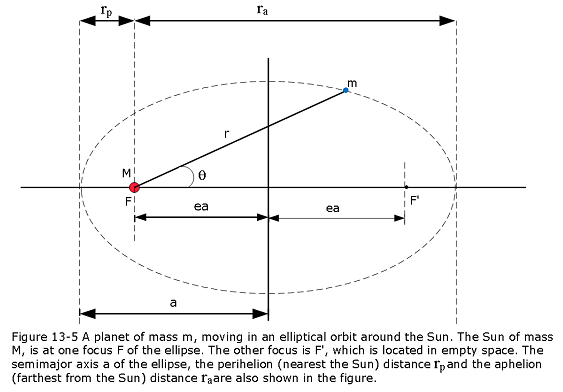
The position vector \(\vec r\) of the planet in terms of polar coordinate is shown in Figure 13-5. In Figure 13-5, the semi-major axis, perihelion (closest to the Sun) and aphelion (farest from the Sun) distances are represented by a, \(R_p\) and \(R_a\) respectively.

\[\begin{equation} \vec r = r\hat e_r \tag{13.22} \end{equation}\]

Thus, the planet’s linear velocity \(\vec v\) becomes

\[\begin{equation} {\vec v} = \frac{d{\vec r}}{dt} = \dot{r}\,{\hat e}_r + r\,\dot{\hat e}_r \tag{13.23} \end{equation}\]

where \(\dot{~}\) is shorthand for \(d/dt\). Note that \({\hat e}_r\) has a non-zero time-derivative (unlike a Cartesian unit vector) because its direction changes as the planet moves around. As is easily demonstrated, from differentiating Eq. 13-10 with respect to time,

\[\begin{equation} \dot{\hat e}_r = \dot{\theta}\,(-\sin\theta,\,\cos\theta) = \dot{\theta}\,\,{\hat e}_\theta. \tag{13.24} \end{equation}\]

Thus, \[\begin{equation} {\vec v} = \dot{r}\,\,{\hat e}_r + r\,\dot{\theta}\,\,{\hat e}_\theta. \tag{13.25} \end{equation}\]

Now, the planet’s acceleration is written

\[\begin{equation} {\vec a} = \frac{d{\vec v}}{dt} = \frac{d^2{\vec r}}{dt^2} = \ddot r \hat e_r + \dot r \dot{\hat e}_r +(\dot r\dot\theta+r\ddot\theta){\hat e}_\theta + r\,\dot{\theta}\,\,\dot{\hat e}_\theta. \tag{13.26} \end{equation}\]

Again, \({\hat e}_\theta\) has a non-zero time-derivative because its direction changes as the planet moves around. Differentiation of Eq. 13-11 with respect to time yields

\[\begin{equation} \dot{\hat e}_\theta = \dot{\theta}\,(-\cos\theta,\,-\sin\theta) = - \dot{\theta}\,{\hat e}_r. \tag{13.27} \end{equation}\]

Hence,

\[\begin{equation} {\vec a} = (\ddot{r}-r\,\dot{\theta}^{\,2})\,{\hat e}_r + (r\,\ddot{\theta} + 2\,\dot{r}\,\dot{\theta})\,{\hat e}_\theta. \tag{13.28} \end{equation}\]

It follows that the equation of motion of our planet, (Eq. 13-4), can be written

\[\begin{equation} {\vec a} = (\ddot{r}-r\,\dot{\theta}^{\,2})\,{\hat e}_r + (r\,\ddot{\theta} + 2\,\dot{r}\,\dot{\theta})\,{\hat e}_\theta = - \frac{G\,M}{r^2}\,{\hat e}_r. \tag{13.29} \end{equation}\]

Since \({\hat e}_r\) and \({\hat e}_\theta\) are mutually orthogonal, we can separately equate the coefficients of both, in the above equation, to give a radial equation of motion,

\[\begin{equation} \ddot{r}-r\,\dot{\theta}^{\,2} = - \frac{G\,M}{r^2}, \tag{13.30} \end{equation}\]

and a tangential equation of motion,

\[\begin{equation} r\,\ddot{\theta} + 2\,\dot{r}\,\dot{\theta} = 0. \tag{13.31} \end{equation}\]

13.0.7 Kepler’s Laws

Planetary motion in the Solar System was first correctly described by astronomer Johannes Kepler in his published works between 1609 and 1619. He described the motion of the Planets in the following three simple laws:

Now let’s see how Kepler’s laws can be explained and derived from Newton’s laws of motion.

13.0.8 Kepler’s First Law:

All planetary orbits are elliptical which are confocal with the Sun (i.e., the Sun lies at one of the focii of each ellipse).

Multiplying both sides of Eq.13-31 by r we get,

\[\begin{equation} r^2\,\ddot{\theta} + 2r\,\dot{r}\,\dot{\theta} = 0. \tag{13.32} \end{equation}\]

Eq. 13-32, can also be expressed as

\[\begin{equation} \frac{d{(r^2\dot\theta)}}{dt}=0 \tag{13.33} \end{equation}\]

Eq. 13-33, implies that

\[\begin{equation} l = r^2\dot\theta = constant \tag{13.34} \end{equation}\]

We already proved this in Eq. 5-39, using Newton’s Third Law of Motion. We have discovered that \(l\) is constant in time and is the angular momentum of our planet. In discussing Newtoian mechanics in Chapter-5 we already mentioned that this is the case because gravity is a central force.

Our planet’s radial equation of motion, (Eq. 13-30), can be combined with Eq.13-34 to give

\[\begin{equation} \ddot{r} -\frac{l^2}{r^3}= - \frac{G\,M}{r^2} \tag{13.35} \end{equation}\]

Suppose that \(r = u^{-1}\). It follows that

\[\begin{equation} \dot{r} = - \frac{\dot{u}}{u^2} = - r^2\,\frac{du}{d\theta}\,\frac{d\theta}{dt} = - l\,\frac{du}{d\theta} \tag{13.36} \end{equation}\]

Similarly,

\[\begin{equation} \ddot{r} = - l \,\frac{d^2 u}{d\theta^2}\,\dot{\theta} = - u^2\,l^2\,\frac{d^2 u}{d\theta^2} \tag{13.37} \end{equation}\]

Hence, Eq. 13-35 can be written in the linear form

\[\begin{equation} \frac{d^2 u}{d\theta^2} + u = \frac{G\,M}{l^2} \tag{13.38} \end{equation}\]

The general solution to the above equation is

\[\begin{equation} u(\theta) = \frac{G\,M}{l^2}\left[1 - e\,\cos(\theta-\theta_0)\right] \tag{13.39} \end{equation}\]

where \(e\) and \(\theta_0\) are arbitrary constants. Without loss of generality, we can set \(\theta_0=0\) by rotating our coordinate system about the \(z\)-axis. Thus, we obtain

\[\begin{equation} r(\theta) = \frac{r_c}{1 - e\,\cos\theta} \tag{13.40} \end{equation}\]

where

\[\begin{equation} r_c = \frac{l^2}{G\,M} \tag{13.41} \end{equation}\]

We find Eq. 13-39 as the equation of a conic section (see Eq. 13-35) which is confocal with the origin (i.e., with the Sun). Specifically, for \(e<1\), Eq. 13-39 is the equation of an ellipse which is confocal with the Sun. Thus, the orbit of our planet around the Sun in a confocal ellipse–this is Kepler’s first law of planetary motion. Of course, a planet cannot have a parabolic or a hyperbolic orbit, since such orbits are only appropriate to objects which are ultimately able to escape from the Sun’s gravitational field.

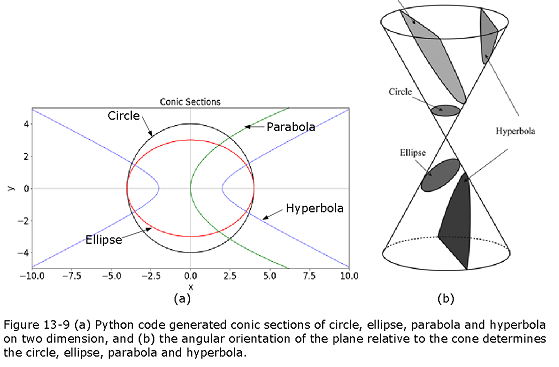
13.0.9 Conic Sections:

The ellipse, the parabola, and the hyperbola are collectively known as conic sections, since these three types of curve can be obtained by taking various different plane sections of a right cone. It turns out that the possible solutions of Eq. 13-30 and 13-31 are all conic sections.

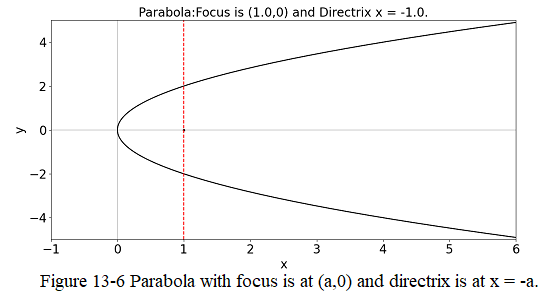
Parabola:

A parabola which is aligned along the \(+x\)-axis, and passes through the origin (see Fig. 13-6).

\[\begin{equation} y^2 - 4ax = 0 \tag{13.42} \end{equation}\]

where \(a>0\).

In the case of the parabola the eccentricity \(e = 1\) For ellipses, the eccentricity \(0 < e < 1\) and it is defined as \[e = \sqrt{\left(1-\frac{b^2}{a^2}\right)}\]

The foci are \(\pm ae,0\) and the directrix are \(x = \pm \frac{a}{e}\)$$

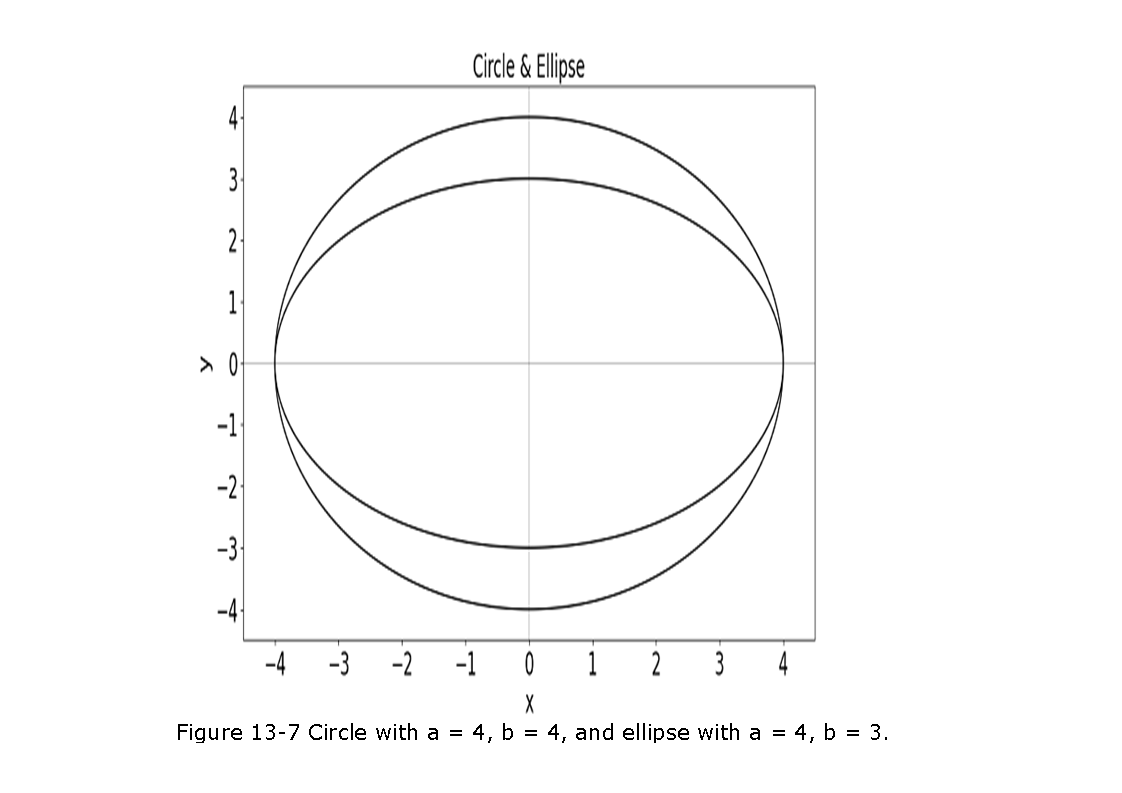
Ellipse:

An ellipse, centered on the origin, of major radius \(a\) and minor radius \(b\), which are aligned along the \(x\)- and \(y\)-axes, respectively (see Fig. 13-2), satisfies the following well-known equation:

\[\begin{equation} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1,\space where\space a>b>0. \tag{13.43} \end{equation}\]

In case of circles a = b. A circle in standard position with an ellipse is shown in Figure 13-7.

Hyperbola:

A hyperbola which is aligned along the \(+x\)-axis, and whose asymptotes intersect at the origin (see Figure 13-8).

\[\begin{equation} \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \tag{13.44} \end{equation}\]

The eccentricity of hyperbola, \[e = \sqrt{\left(1-\frac{b^2}{a^2}\right)}\] The foci and directrices are the same as the ellipsis and the asymptotes can be found at \(y=\pm \frac{b}{a}x\).

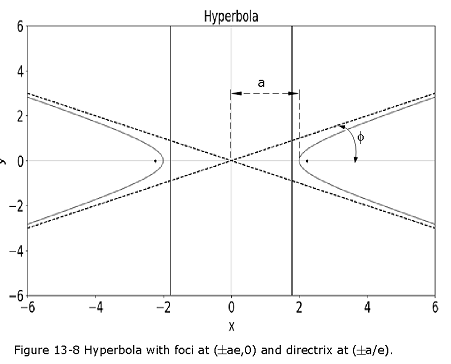
In Figure-13-8, \(a\) is the distance of closest approach to the origin. The asymptotes subtend an angle \(\phi=\tan^{-1}(b/a)\) with the \(x\)-axis. All conic sections can be described in terms of eccentricity. Satellite orbits are any of the four conic sections. All conic sections are have semi-major axis and the energy. The Table 13-3 shows the type of conic sections and their relationships with eccentricity, semi-major axis, and energy.

Table 13-3 Conic Section Parameters

Conic Section	Eccentricity, e	Semi-major Axis	Energy
Circle	0	a=Radius	E<0
Ellipse	0 < e < 1	a>0	E<0
Parabola	e = 1	a=Infinity	E=0
Hyperbola	e > 1	a<0	E>0

In summarizing the discussion on conic section, or just conic, is a curve formed by passing a plane through a right circular cone. As shown in Figure 13-9, the angular orientation of the plane relative to the cone determines whether the conic section is a circle, ellipse, parabola, or hyperbola. The circle and the ellipse arise when the intersection of cone and plane is a bounded curve. The circle is a special case of the ellipse in which the plane is perpendicular to the axis of the cone. If the plane is parallel to a generator line of the cone, the conic is called a parabola. If the intersection is an unbounded curve and the plane is not parallel to a generator line of the cone, the figure is a hyperbola. In the latter case the plane will intersect both halves of the cone, producing two separate curves.

Now what are common characteristics among the ellipse, the parabola, and the hyperbola (other than being conic sections). These three curves can all be represented as the locus of a movable point whose distance from a fixed point is in a constant ratio to its perpendicular distance to some fixed straight-line. Let the fixed point (which is termed the focus of the ellipse/parabola/hyperbola) lie at the origin, and let the fixed line correspond to \(x=-d\) (with \(d>0\)). Thus, the distance of a general point (\(x\), \(y\)) (which lies to the right of the line \(x=-d\)) from the origin is \(r_1=\sqrt{x^2+y^2}\), whereas the perpendicular distance of the point from the line \(x=-d\) is \(r_2 = x+d\) as shown in Figure 13-10.

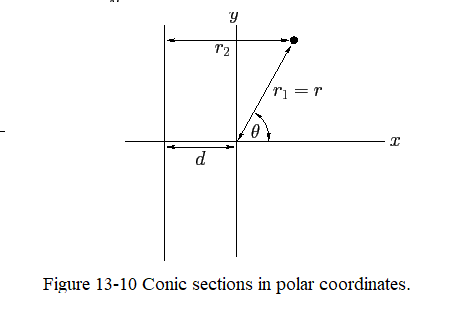
In polar coordinates, \(r_1=r\) and \(r_2 = r\,\cos\theta+d\). Hence, the locus of a point for which \(r_1\) and \(r_2\) are in a fixed ratio satisfies the following equation:

\[\begin{equation} \frac{r_1}{r_2} = \frac{\sqrt{x^2+y^2}}{x+d}= \frac{r}{r\,\cos\theta+d}=e, \tag{13.45} \end{equation}\]

where \(e\geq 0\) is a constant. When expressed in terms of polar coordinates, the above equation can be rearranged to give

\[\begin{equation} r = \frac{r_c}{1-e\,\cos\theta}, \tag{13.46} \end{equation}\]

where \(r_c=e\,d\).

When written in terms of Cartesian coordinates, can be rearranged to give

\[\begin{equation} \frac{(x-x_c)^2}{a^2} + \frac{y^2}{b^2} = 1, \tag{13.47} \end{equation}\]

for \(e<1\).

Here, \[\begin{equation} \displaystyle a \textstyle =\displaystyle \frac{r_c}{1-e^2}, \tag{13.48} \end{equation}\]

\[\begin{equation} \displaystyle b \textstyle = \displaystyle \frac{r_c}{\sqrt{1-e^2}}=\sqrt{1-e^2}\,a, \tag{13.49} \end{equation}\]

\[\begin{equation} \displaystyle x_c \textstyle =\displaystyle \frac{e\,r_c}{1-e^2}= e\,a. \tag{13.50} \end{equation}\]

Table 13-3 Some Properties of the Planets

	Mercury	Venus	Earth	Mars	Jupiter	Saturn	Uranus	Neptune	Pluto\(^d\)
\(Mean~distance\)\(~from~Sun,\)\(~10^6 km\)	57.9	108	150	228	778	1430	2870	4500	5900
Eccentricity of orbits	0.206	0.0068	0.0167	0.0934	0.0485	0.0556	0.0472	0.0086	0.250
Period of revolution, y	0.241	0.615	1.00	1.88	11.9	29.5	84.0	165	248
Period of rotation,\(^a\) d	55.7	-243\(^b\)	0.997	1.03	0.409	0.436	-0.451\(^b\)	0.658	6.39
Orbital speed, km/s	47.9	35.0	29.8	24.1	13.1	9.64	6.81	5.43	4.74
Inclination of axis to orbit, degree	\(< 28^\circ\)	\(\approx 3^\circ\)	\(23.4^\circ\)	\(25.0^\circ\)	\(3.08^\circ\)	\(26.7^\circ\)	\(97.9^\circ\)	\(29.6^\circ\)	\(57.5^\circ\)

\(^a\) Measured with respect to distant stars.

\(^b\) Venus and Urenus rotate opposite their orbital motion.

\(^c\) Gravitational acceleration measured at the planet’s equator.

\(d\) Pluto is a dwarf planet.

Running a python code to plot Eq. 13-57 using the eccentricity data as given in Table-13-3, we can visualize how the trajectories change as can be seen in Figure 13-11.

In Figure 13-11, Earth’s orbit is indicated with red color and Pluto’s orbit has black color and is the farthest from the Sun. Planetary orbits described here are kind of simplified picture of the actual reality. <>

An orbit in reality has six parameters, called orbital elements. They are

Semi-Major Axis, a

Eccentricity, e

Inclination, i

Argument of Periapsis, \(\omega\)

Time of Periapsis Passage, T

Longitude of Ascending Node, \(\Omega\)

An orbiting satellite or planet moves on an elliptical path with the body being orbited, called the primary, located at one of two points called foci.

Inclination is the angular distance between a satellite’s orbital plane and the equator of its primary (or the ecliptic plane in the case of heliocentric, or sun centered, orbits). An inclination of zero degrees indicates an orbit about the primary’s equator in the same direction as the primary’s rotation. An inclination of 90 degrees indicates a polar orbit. An inclination of 180 degrees indicates a retrograde equatorial orbit. A retrograde orbit is one in which a satellite moves in a direction opposite to the rotation of its primary.

Periapsis is the point in an orbit closest to the primary. The farthest point in an orbit, is called apoapsis. Periapsis and apoapsis are usually modified to apply to the body being orbited, such as perihelion and aphelion for the Sun, perigee and apogee for Earth, perijove and apojove for Jupiter, perilune and apolune for the Moon, etc.

Nodes are the points where an orbit crosses a plane, such as a satellite crossing the Earth’s equatorial plane. If the satellite crosses the plane going from south to north, the node is the ascending node; if moving from north to south, it is the descending node. The longitude of the ascending node is the node’s celestial longitude. Celestial longitude is analogous to longitude on Earth and is measured in degrees counter-clockwise from zero with zero longitude being in the direction of the vernal equinox.

Types Of Orbits:

For a spacecraft to achieve Earth orbit, it must be launched to an elevation above the Earth’s atmosphere and accelerated to orbital velocity. The most energy efficient orbit, that is one that requires the least amount of propellant, is a direct low inclination orbit. To achieve such an orbit, a spacecraft is launched in an eastward direction from a site near the Earth’s equator. The advantage being that the rotational speed of the Earth contributes to the spacecraft’s final orbital speed. At the United States’ launch site in Cape Canaveral (28.5 degrees north latitude) a due east launch results in a “free ride” of 1,471 km/h (914 mph). Launching a spacecraft in a direction other than east, or from a site far from the equator, results in an orbit of higher inclination. High inclination orbits are less able to take advantage of the initial speed provided by the Earth’s rotation, thus the launch vehicle must provide a greater part, or all, of the energy required to attain orbital velocity. Although high inclination orbits are less energy efficient, they do have advantages over equatorial orbits for certain applications. Below we describe several types of orbits and the advantages of each:

Geosynchronous orbits (GEO) are circular orbits around the Earth having a period of 24 hours. A geosynchronous orbit with an inclination of zero degrees is called a geostationary orbit. A spacecraft in a geostationary orbit appears to hang motionless above one position on the Earth’s equator. For this reason, they are ideal for some types of communication and meteorological satellites. To attain geosynchronous orbit, a spacecraft is first launched into an elliptical orbit with an apogee of 35,786 km (22,236 miles) (see Solved Problem-5) called a geosynchronous transfer orbit (GTO). The orbit is then circularized by firing the spacecraft’s engine at apogee.

Polar orbits (PO) are orbits with an inclination of 90 degrees. Polar orbits are useful for satellites that carry out mapping and/or surveillance operations because as the planet rotates the spacecraft has access to virtually every point on the planet’s surface.

Walking orbits An orbiting satellite is subjected to a great many gravitational influences. First, planets are not perfectly spherical and they have slightly uneven mass distribution. These fluctuations have an effect on a spacecraft’s trajectory. Also, the sun, moon, and planets contribute a gravitational influence on an orbiting satellite. With proper planning it is possible to design an orbit which takes advantage of these influences to induce a precession in the satellite’s orbital plane. The resulting orbit is called a walking orbit, or precessing orbit.

Sun synchronous orbits (SSO) are walking orbits whose orbital plane precesses with the same period as the planet’s solar orbit period. In such an orbit, a satellite crosses periapsis at about the same local time every orbit. This is useful if a satellite is carrying instruments which depend on a certain angle of solar illumination on the planet’s surface. In order to maintain an exact synchronous timing, it may be necessary to conduct occasional propulsive maneuvers to adjust the orbit.

Molniya orbits are highly eccentric Earth orbits with periods of approximately 12 hours (2 revolutions per day). The orbital inclination is chosen so the rate of change of perigee is zero, thus both apogee and perigee can be maintained over fixed latitudes. This condition occurs at inclinations of 63.4 degrees and 116.6 degrees. For these orbits the argument of perigee is typically placed in the southern hemisphere, so the satellite remains above the northern hemisphere near apogee for approximately 11 hours per orbit. This orientation can provide good ground coverage at high northern latitudes.

Hohmann transfer orbits are interplanetary trajectories whose advantage is that they consume the least possible amount of propellant. A Hohmann transfer orbit to an outer planet, such as Mars, is achieved by launching a spacecraft and accelerating it in the direction of Earth’s revolution around the sun until it breaks free of the Earth’s gravity and reaches a velocity which places it in a sun orbit with an aphelion equal to the orbit of the outer planet. Upon reaching its destination, the spacecraft must decelerate so that the planet’s gravity can capture it into a planetary orbit.

To send a spacecraft to an inner planet, such as Venus, the spacecraft is launched and accelerated in the direction opposite of Earth’s revolution around the sun (i.e. decelerated) until it achieves a sun orbit with a perihelion equal to the orbit of the inner planet. It should be noted that the spacecraft continues to move in the same direction as Earth, only more slowly.

To reach a planet requires that the spacecraft be inserted into an interplanetary trajectory at the correct time so that the spacecraft arrives at the planet’s orbit when the planet will be at the point where the spacecraft will intercept it. This task is comparable to a quarterback “leading” his receiver so that the football and receiver arrive at the same point at the same time. The interval of time in which a spacecraft must be launched in order to complete its mission is called a launch window.

13.0.10 Kepler’s Second Law:

The radius vectors connecting each planet to the Sun sweep out equal areas in equal time intervals.

Multiplying the planet’s tangential equation of motion, Eq. 13-21, by \(r\), we obtain

\[\begin{equation} r^2\,\ddot{\theta} + 2\,r\,\dot{r}\,\dot{\theta} = 0 \tag{13.51} \end{equation}\]

However, the above equation can be also written

\[\begin{equation} \frac{d(r^2\,\dot{\theta})}{dt} = 0, \tag{13.52} \end{equation}\]

which implies that

\[\begin{equation} l = r^2\,\dot{\theta} \tag{13.53} \end{equation}\]

is constant in time. It is easily demonstrated that \(l\) is the magnitude of the vector \({\vec l}\) defined in Eq. 13-8. Thus, the fact that \(l\) is constant in time is equivalent to the statement that the angular momentum of our planet is a constant of its motion. As we have already mentioned, this is the case because gravity is a central force.

Suppose that the radius vector connecting our planet to the origin (i.e., the Sun) sweeps out an angle \(\Delta\theta\) between times \(t\) and \(t+\Delta t\)–see Figure 13-6. The approximately triangular region swept out by the radius vector has the area

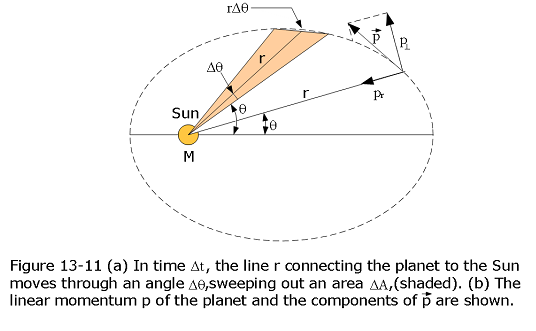
\[\begin{equation} \Delta A \simeq \frac{1}{2}(r\Delta\theta)r, \tag{13.54} \end{equation}\]

since the area of a triangle is half its base ( \(r\,\Delta\theta\)) times its height (\(r\)). Hence, the rate at which the radius vector sweeps out area is

\[\begin{equation} \frac{dA}{dt} = \lim_{\Delta t\rightarrow 0}\frac{r^2\Delta\theta}{\Delta{t}}= \frac{r^2}{2}\,\frac{d\theta}{dt} = \frac{l}{2} \tag{13.55} \end{equation}\]

Thus, the radius vector sweeps out area at a constant rate (since \(l\) is constant in time)–this is Kepler’s second law. We conclude that Kepler’s second law of planetary motion is a direct consequence of angular momentum conservation.

13.0.11 Kepler’s Third Law:

The squares of the orbital periods of the planets are proportional to the cubes of their orbital major radii.

We have seen that the radius vector connecting our planet to the origin sweeps out area at the constant rate \(dA/dt=l/2\) [see Eq. 13-40]. We have also seen that the planetary orbit is an ellipse. Suppose that the major and minor radii of the ellipse are \(a\) and \(b\), respectively. It follows that the area of the ellipse is \(A=\pi\,a\,b\). Now, we expect the radius vector to sweep out the whole area of the ellipse in a single orbital period, \(T\). Hence,

\[\begin{equation} T = \frac{A}{(dA/dt)} = \frac{2\pi\,a\,b}{l} \tag{13.56} \end{equation}\]

It follows from Eqns. (13-37), (13-38), and (13-30) that

\[\begin{equation} T^2 = \frac{4\pi^2\,a^3}{G\,M} \tag{13.57} \end{equation}\]

In other words, the square of the orbital period of our planet is proportional to the cube of its orbital major radius–this is Kepler’s third law.

Note that for an elliptical orbit the closest distance to the Sun–the so-called perihelion distance–is [see Equations (236) and (255)]

\[\begin{equation} r_p = \frac{r_c}{1+e} = a\,(1-e) \tag{13.58} \end{equation}\]

Likewise, the furthest distance from the Sun–the so-called aphelion distance–is

\[\begin{equation} r_a = \frac{r_c}{1-e} = a\,(1+e) \tag{13.59} \end{equation}\]

It follows that the major radius, \(a\), is simply the mean of the perihelion and aphelion distances,

\[\begin{equation} a = \frac{r_p+r_a}{2} \tag{13.60} \end{equation}\]

The parameter

\[\begin{equation} e = \frac{r_a-r_p}{r_a+r_p} \tag{13.61} \end{equation}\]

is called the eccentricity, and measures the deviation of the orbit from circularity. Thus, \(e=0\) corresponds to a circular orbit, whereas \(e\rightarrow 1\) corresponds to an infinitely elongated elliptical orbit.

As is easily demonstrated from the above analysis, Kepler laws of planetary motion can be written in the convenient form

\[\begin{equation} \displaystyle r \textstyle = \displaystyle \frac{a\,(1-e^2)}{1-e\,\cos\theta}, \tag{13.62} \end{equation}\]

\[\begin{equation} \displaystyle r^2\,\dot{\theta} \textstyle = \displaystyle (1-e^2)^{1/2}\,\omega\,a^2, \tag{13.63} \end{equation}\]

\[\begin{equation} \displaystyle G\,M \textstyle = \displaystyle \omega^2\,a^3, \tag{13.64} \end{equation}\]

where \(a\) is the mean orbital radius (i.e., the major radius), \(e\) the orbital eccentricity, and \(\omega=2\pi/T\) the mean orbital angular velocity.

Example Problem 13-1: Halley’s comet has an and a perihelion distance of \(r_p = 8.9 \times 10^{10}\) m. Find (a) the orbital period, and (b) the comet’s speed at perihelion and aphelion.

Solution:

1. Given the orbital eccentricity of \(e=0.967\), and the perihelion distance of \(r_p = 8.9 \times 10^{10}\) m, we can find the semimajor axis using Figure 13-5 as follows:

\[a = \frac{r_p}{(1-e)}=\frac{8.9 \times 10^{10}}{(1-0.967)}=2.697 \times 10^{12}\] m

Now we can find the orbital period using Eq. 13-57,

\[T = \sqrt{\frac{4\pi^2a^3}{GM}} =\sqrt{\frac{4\pi^2(2.697\times 10^{12}m)^3}{(6.673\times 10^{-11}m^3/kg-s^2)(1.99\times 10^{30}kg)}} =2.415\times 10^9\space s=76.53\space yrs\space(Answer)\]

2. To calculate the comet’s speed at perihelion and aphelion, we first need to find the aphelion distance.

\[r_a=2a-r_p=2(2.697\times 10^{12}-8.9\times 10^{10}=5.305\times 10^{12}\space m\]

Velocity at perihelion distance: \[v_p=\sqrt{GM(\frac{2}{r_p}-\frac{1}{a})} =\sqrt{(6.673\times 10^{-11}\space m^3/kg-s^2)(1.99\times 10^{30}\space kg)\left(\frac{2} {8.9\times 10^{10}\space m}-\frac{1}{2.697\times 10^{12}\space m}\right)}=54.19\space \frac{km}{s}\space(Answer)\]

Velocity at aphelion distance: \[v_a=\sqrt{GM(\frac{2}{r_a}-\frac{1}{a})}=\sqrt{(6.673\times 10^{-11}\space m^3/kg-s^2)(1.99\times 10^{30} \space kg)\left(\frac{2}{5.31\times 12^{10}\space m}-\frac{1}{2.697\times 10^{12}\space m}\right)}=0.89\space \frac{km}{s}\space(Answer)\]

So, the speed of the comet at the perihelion distance is 54.19 km/s and at the aphelion distance is 0.89 km/s. The velocity at the perihelion distance is 60.89 times more than at aphelion distance. This makes sense since comet is closest to Sun at perihelion distance is stronly influenced by Sun’s gravitational field.

13.0.12 Satellites: Orbits and Energy:

According to Equations (13-17) and (13-25), the total energy per unit mass of an object in orbit around the Sun is given by

\[\begin{equation} {\cal E} = \frac{v^2}{2}-\frac{GM}{r}=\frac {\dot{r}^{\,2} + r^2\,\dot{\theta}^{\,2}}{2} - \frac{G\,M}{r}. \tag{13.65} \end{equation}\]

Here we made use of \[(\vec v\cdot\vec v)=(\hat e_r\vec{\dot{r}}+\vec r\dot{\theta}\hat e_{\theta})\cdot(\hat e_r\vec{\dot{r}} +\vec r\dot{\theta}\hat e_{\theta})=\dot{r}^2+r^2\dot{\theta}^2\]

It follows from Equations (13-35), (13-36), and (13-41) that

\[\begin{equation} {\cal E} = \frac{l^2}{2}\left[\left(\frac{du}{d\theta}\right)^2 + u^2 - 2\,u\,u_c\right], \tag{13.66} \end{equation}\]

where \(u=r^{-1}\), and \(u_c = r_c^{-1}\). However, according to Equation (13-40),

\[\begin{equation} u(\theta) = u_c\,(1-e\,\cos\theta). \tag{13.67} \end{equation}\]

The previous two equations can be combined with Equations (13-41) and (13-58) to give

\[\begin{equation} {\cal E} = \frac{u_c^{\,2}\,l^2}{2}\, (e^2 -1) = \frac{G\,M}{2\,r_p}\,(e-1). \tag{13.68} \end{equation}\]

We conclude that elliptical orbits (\(e<1\)) have negative total energies, whereas parabolic orbits (\(e=1\)) have zero total energies, and hyperbolic orbits (\(e>1\)) have positive total energies. This makes sense, since in a conservative system in which the potential energy at infinity is set to zero [see Equation (13-16)] we expect bounded orbits to have negative total energies, and unbounded orbits to have positive total energies. Thus, elliptical orbits, which are clearly bounded, should indeed have negative total energies, whereas hyperbolic orbits, which are clearly unbounded, should indeed have positive total energies. Parabolic orbits are marginally bounded (i.e., an object executing a parabolic orbit only just escapes from the Sun’s gravitational field), and thus have zero total energy. For the special case of an elliptical orbit, whose major radius \(a\) is finite, we can write

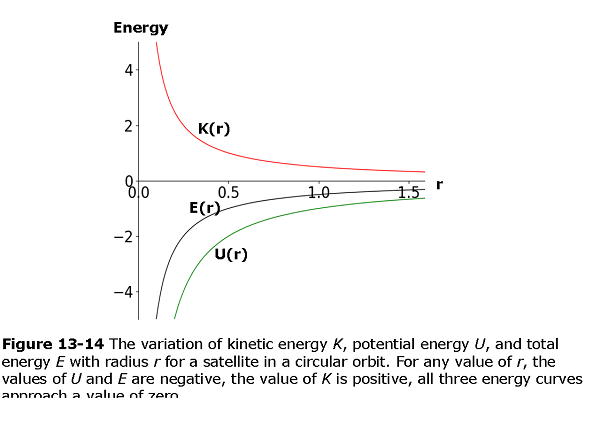
\[\begin{equation} {\cal E} = - \frac{G\,M}{2\,a}. \tag{13.69} \end{equation}\]

It follows that the energy of such an orbit is completely determined by the orbital major radius. Consider an artificial satellite in an elliptical orbit around the Sun (the same considerations also apply to satellites in orbit around the Earth). At perihelion, \(\dot{r}=0\), and Equations (13-65) and (13-68) can be combined to give

\[\begin{equation} \frac{v_t}{v_c} = \sqrt{1+e}. \tag{13.70} \end{equation}\]

Here, \(v_t=r\,\dot{\theta}\) is the satellite’s tangential velocity, and \(v_c=\sqrt{G\,M/r_p}\) is the tangential velocity that it would need in order to maintain a circular orbit at the perihelion distance. Likewise, at aphelion,

\[\begin{equation} \frac{v_t}{v_c} = \sqrt{1-e}, \tag{13.71} \end{equation}\]

where \(v_c=\sqrt{G\,M/r_a}\) is now the tangential velocity that the satellite would need in order to maintain a circular orbit at the aphelion distance. Suppose that our satellite is initially in a circular orbit of radius \(r_1\), and that we wish to transfer it into a circular orbit of radius \(r_2\), where \(r_2> r_1\). We can achieve this by temporarily placing the satellite in an elliptical orbit whose perihelion distance is \(r_1\), and whose aphelion distance is \(r_2\). It follows, from Equation (13-61), that the required eccentricity of the elliptical orbit is

\[\begin{equation} e = \frac{r_2-r_1}{r_2+r_1}. \tag{13.72} \end{equation}\]

According to Equation (13-70), we can transfer our satellite from its initial circular orbit into the temporary elliptical orbit by increasing its tangential velocity (by briefly switching on the satellite’s rocket motor) by a factor

\[\begin{equation} \alpha_1 = \sqrt{1+e}. \tag{13.73} \end{equation}\]

We must next allow the satellite to execute half an orbit, so that it attains its aphelion distance, and then boost the tangential velocity by a factor [see Equation (13-71)]

\[\begin{equation} \alpha_2 = \frac{1}{\sqrt{1-e}}. \tag{13.74} \end{equation}\]

The satellite will now be in a circular orbit at the aphelion distance, \(r_2\). This process is illustrated in Figure 13-7.

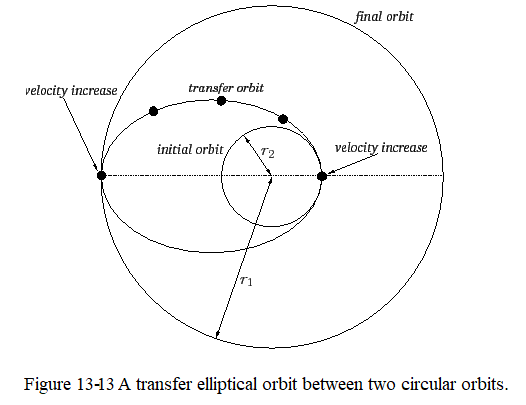
Obviously, we can transfer our satellite from a larger to a smaller circular orbit by performing the above process in reverse. Note, finally, from Equation (13-61), that if we increase the tangential velocity of a satellite in a circular orbit about the Sun by a factor greater than \(\sqrt{2}\) then we will transfer it into a hyperbolic orbit (\(e>1\)), and it will eventually escape from the Sun’s gravitational field.

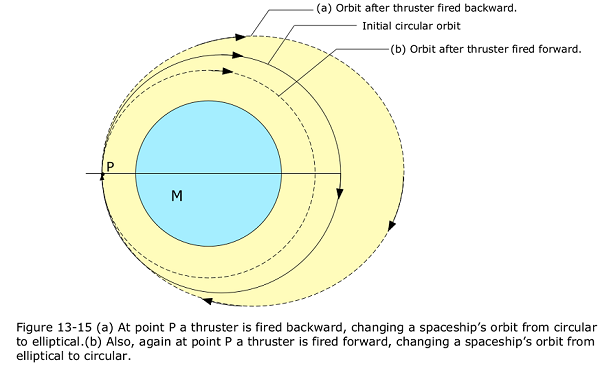
Example Problem 13-2 Transforming a circular orbit into an elliptical orbit

1. A spaceship of mass \(m = 4.50 \times 10^3\) kg is in a circular Earth orbit of radius \(r = 8.00 \times 10^6\) m and period \(T_0 = 118.6\) min = \(7.119 \times 10^3\) s when a thruster is fired in the backward direction to increase the speed to 5.0% of the original speed. (b) What is the period T of the resulting elliptical orbit (Fig. 13-17)? Instead a thruster is fired in the forward direction to decrease the speed to 95% of the original speed. (b) What is the period T of the resulting elliptical orbit (Fig. 13-17)?

Solution:

1. A thruster is fired in the backward direction to increase the speed to 5.0% of the original speed:

\[K = \frac{1}{2}mv^2=\frac{1}{2}m(1.05v_0)^2 =\frac{1}{2}(4.50\times 10^3\space kg)(1.05)^2\left(\frac{2\pi(8.00\times 10^6\space m)}{7.119\times 10^3\space s}\right)^2 = 1.237\times 10^{11}\space J\]

Just after firing the thruster, the spaceship is still at orbital radius r, and its gravitational potential energy is

\[U=-\frac{GMm}{r}=-\frac{(6.67\times 10^{-11}N-m^2/kg^2)(5.98\times 10^{24}kg)(4.50\times 10^3kg)} {8.00\times 10^6m}=-2.2436\times 10^{11}J\]

We can find the semimajor axis from Eq. 13-69, by substituting the result of energy as we calculated above:

\[a=-\frac{GMm}{2E}=-\frac{GMm}{2(K+U)}=-\frac{(6.67\times 10^{-11}N-m^2/kg^2)(5.98\times 10^{24}kg) (4.50\times 10^3kg)}{2(1.237\times 10^11J-2.2426\times 10^{11}J}=8.9245\times 10^6 m\]

We substitute the result of a in Eq. 13-57, to calculate the period T as follows:

\[T=\sqrt{\left(\frac{4\pi^2a^3}{GM}\right)}=\left(\frac{4\pi^2(8.9245\times 10^6m)^3} {(6.67\times10^{-11}N-m^2/kg^2)(5.98\times 10^{24}kg)}\right)^{1/2}=8.388\times 10^3\space s =139.795\space min\space (Answer)\]

This period is for an elliptical orbit that spaceship takes after the thruster is fired in the backward direction. This period is much longer than the period of \(T_0\) for the circular orbit two reasons. (1) The orbital path length is now more. (2) The elliptical path takes the spaceship far from Earth everywhere except at the point of firing (Fig. 13-14). The resulting increase in gravitational potential energy decreases the kinetic energy and thus also the speed of the spaceship.

2. Repeating (a) now for decreasing the speed of the spaceship by 5%, we get \[K = \frac{1}{2}mv^2=\frac{1}{2}m(0.95v_0)^2 =\frac{1}{2}(4.50\times 10^3\space kg)(0.95)^2\left(\frac{2\pi(8.00\times 10^6\space m)}{7.119\times 10^3\space s}\right)^2 = 1.0124\times 10^{11}\space J\]

Just after firing the thruster, the spaceship is still at orbital radius r, and its gravitational potential energy is

\[U=-\frac{GMm}{r}=-\frac{(6.67\times 10^{-11}N-m^2/kg^2)(5.98\times 10^{24}kg)(4.50\times 10^3kg)}{8.00\times 10^6m} =-2.2436\times 10^{11}J\]

We can find the semimajor axis from Eq. 13-69, by substituting the result of energy as we calculated above:

\[a=-\frac{GMm}{2E}=-\frac{GMm}{2(K+U)}=-\frac{(6.67\times 10^{-11}N-m^2/kg^2)(5.98\times 10^{24}kg)(4.50\times 10^3kg)}{2(1.0124\times 10^11J-2.2426\times 10^{11}J} =7.289\times 10^6 m\]

We substitute the result of a in Eq. 13-57, to calculate the period T as follows:

\[T=\sqrt{\left(\frac{4\pi^2a^3}{GM}\right)}=\left(\frac{4\pi^2(7.289\times 10^6m)^3}{(6.67\times10^{-11}N-m^2/kg^2)(5.98\times 10^{24}kg)}\right)^{1/2} =6.191\times 10^3\space s=103.185\space min\space (Answer)\]

This period is for an elliptical orbit that spaceship takes after the thruster is fired in the forward direction. This period is much less than the period of \(T_0\) for the circular orbit two reasons. (1) The orbital path length is now less. (2) The elliptical path takes the spaceship closer from Earth everywhere except at the point of firing (Fig. 13-14. The resulting decrease in gravitational potential energy increases the kinetic energy and thus also the speed of the spaceship.

Solved Problems: 1. [21] Certain neutron stars (extremely dense stars) are believed to be rotating at about 1 rev/s. If such a star has a radius of 20 km, what must be its minimum mass so that material on its surface remains in place during the rapid rotation?

Solution: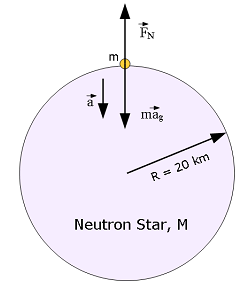

Net radial force acting on m, \(F_{net,r}=ma_r\)

\[F_N-ma_g=m(-\omega^2R)\] \[mg=ma_g-m\omega^2R\] \[g=a_g-\omega^2R\] By the given condition for m to remain in place, \[0=a_g-\omega^2R\] \[0=\frac{GM}{R^2}-\omega^2R\] \[M=\frac{R^3\omega^2}{G} =\frac{(20\times 10^3\space m)^3)(2\pi\space rad/s)^2}{6.67\times 10^{-11}\frac{m^3}{kg-s^2}}\approx 4.74\times 10^24\space kg\space(Answer)\]

The mass of neutron star comes out to be in the same order of magnitude as Earth. Earth has radius, \(6370\space km\), whereas the neutron star has radius only \(20\space km\).

2. [22] The radius \(R_h\) and mass \(M_h\) of a black hole are related by \(R_h = 2GM_h/c^2\), where c is the speed of light. Assume that the gravitational acceleration \(a_g\) of an object at a distance \(r_0 = 1.001R_h\) from the center of a black hole is given by Eq. 13-7 (it is, for large black holes). (a) In terms of \(M_h\), find \(a_g\) at \(r_0\). (b) Does \(a_g\) at \(r_0\) increase or decrease as \(M_h\) increases? (c) What is \(a_g\) at \(r_0\) for a very large black hole whose mass is \(1.55 \times 10^{12}\) times the solar mass of \(1.99 \times 10^{30}\) kg? (d) If an astronaut of height 1.70 m is at \(r_0\) with her feet down, what is the difference in gravitational acceleration between her head and feet?

5. Is the tendency to stretch the astronaut severe?

Solution: (a) From Eq. 13-7, gravitational acceleration, \(a_g=\frac{GM_h}{r_0^2}\).

Plug in \(M_h = \frac{R_hc^2}{2G}\), and \(r_0 = 1.001R_h\) in Eq. 13-7, we get

\[a_g=\frac{c^2}{2(1.001)^2R_h}=\frac{c^2}{2(1.001)^2\frac{2GM_h}{c^2}}=\frac{c^4}{4GM_h(1.001)^2} =\frac{(3\times 10^8\space m/s)^4}{4\left(6.67\times 10^{-11}\space \frac{m^3}{kg-s^2}\right)(1.001)^2M_h} =\frac{3.03\times 10^{43}\space\frac{kg-m}{s^2}}{M_h}\space(Answer)\]

2. \(M_h\) increases \(a_g\) decreases.

3. Given \(M_h=(1.55 \times 10^{12})(1.99 \times 10^{30}\) kg)$, we can recalculate \(a_g\) as follows:

\[a_g=\frac{c^4}{4GM_h(1.001)^2}=\frac{3\times 10^{43}\space\frac{kg-m}{s^2}}{M_h}\space =\frac{3.03\times 10^{43}\space\frac{kg-m}{s^2}}{(1.55 \times 10^{12})(1.99 \times 10^{30})\space kg)} =9.82\space m/s^2(Answer)\]

4. To answer the gravitational acceleration between astronauts her head and feet we need to differentiate Eq. 13-7, as follows:

\(da_g=\frac{-2GM_h}{r^3}dr\), substituting, \(r=r_0=(1.001)(R_h)=(1.001)\frac{2GM_h}{c^2}\)

\[da_g=\frac{-2GM_h}{r^3}dr=\frac{-2GM_hdr}{\frac{(2.002)^3M_h^3G^3}{c^6}} =\frac{-2c^6dr}{(2.002)^3M_h^2G^2} =\frac{-2(3\times 10^8\space m/s)^6(1.7\space m)}{(2.002)^3((1.55\times 10^12)(1.99\times10^{30}\space kg)^2)^2)(6.67\times10^{-11}\frac{m^3}{kg-s^2}} =-7.27\times 10^{-15}\space m/s^2\space(Answer)\]

5. The result of (d) shows that by stretching of astronaut’s body will have no effect.

3. [27] Figure 13-42 shows, not to scale, a cross section through the interior of Earth. Rather than being uniform throughout, Earth is divided into three zones: an outer crust, a mantle, and an inner core. The dimensions of these zones and the masses contained within them are shown on the figure. Earth has a total mass of \(5.98 \times 10^{24}\) kg and a radius of 6370 km. Ignore rotation and assume that Earth is spherical.

1. Calculate \(a_g\) at the surface. (b) Suppose that a bore hole (the Mohole) is driven to the crust – mantle interface at a depth of 25.0 km; what would be the value of \(a_g\) at the bottom of the hole? (c) Suppose that Earth were a uniform sphere with the same total mass and size.What would be the value of \(a_g\) at a depth of 25.0 km? (Precise measurements of \(a_g\) are sensitive probes of the interior structure of Earth, although results can be clouded by local variations in mass distribution.)

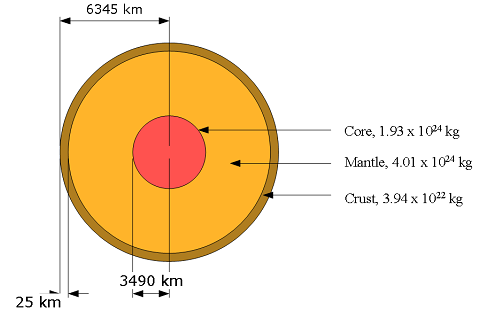
Solution:

1. \[F=\frac{GM_m}{R^2}\] \[ma_g=\frac{GM_m}{R^2}\] \[a_g=\frac{GM}{R^2} =\frac{(6.67\times10^{-11}\frac{m^3}{s^2-kg})(5.98\times 10^{24}\space kg)}{(6.37\times10^6\space m)^2}=9.83\space m/s^2\space(Answer)\]

2. \[a_g=\frac{G(M_{core}+M_{mantle})}{R_{(c+m)}^2} =\frac{(6.67\times10^{-11}\frac{m^3}{s^2-kg})(1.93\times 10^{24}\space kg+4.01\times 10^{24}\space kg)}{(6.345\times10^6\space m)^2}=9.84\space m/s^2\space(Answer)\]

3. \[a_g=\frac{GM}{R_{(c+m)}^2}\] Assuming that Earth is a uniform sphere with the same total mass and size, then \[\frac{M_E}{V_E}=\rho$ and $\frac{M}{V_{c+m}}=\rho$, then \]M=M_E() =M_E()=M_E()^3$$

Therefore, the new mass can be calculated as follows: \[M=M_E\left(\frac{R_{c+m}}{R_E}\right)^3 =(5.98\times 10^{24}\space kg)\left(\frac{6.345\times 10^6\space m}{6.37\times 10^6\space m}\right)^3=5.9\times 10^{24}\space kg\] Hence, \[a_g=\frac{GM}{R_{(c+m)}^2} =\frac{(6.67\times10^{-11}\frac{m^3}{s^2-kg})(5.91\times 10^{24}\space kg)}{(6.345\times10^6\space m)^2}=9.79\space m/s^2\space(Answer)\]

4. [44] A satellite is put in a circular orbit about Earth with a radius equal to one-half the radius of the Moon’s orbit. What is its period of revolution in lunar months? (A lunar month is the period of revolution of the Moon.)

Solution: Using Kepler’s third law of period, \[T_s^2=\left(\frac{4\pi ^2}{GM}\right)r_s^3\], and \[T_m^2=\left(\frac{4\pi ^2}{GM}\right)r_m^3\], where subscripts s and m denote the satellite and moon respectively. Taking ratio, we get \[T_s=\frac{T_m}{\sqrt 8}=0.353T_m\]

Since 1 lunar month = 29.53059 days, therefore, \[T_s =\frac{T_m}{\sqrt 8}=(0.353)(29.53059 \space days)=10.42\space days\space (Answer)\]

5. [50] An orbiting satellite stays over a certain spot on the equator of (rotating) Earth. What is the altitude of the orbit (called a geosynchronous orbit)?

Solution: To keep the satellite in a geosynchronous orbit, period of revolution of satellite must be T = 24 h.

So, using Kepler’s third law of period, the altitude of the satellite from the center of the Earth is \[r=\left(\frac{T^2GM}{4\pi^2}\right)^{1/3} =\left(\frac{(86400\space)^2(6.67\times 10^{-11}\frac{m^3}{kg-s^2})(5.98\times 10^{24}\space kg)}{4\pi ^2}\right)^{1/3}=42.176\times 10^6\space m\]

Therefore, satellite must be placed at an altitude \(h = r-r_E\), where \(r_E\) is the radius of Earth. Thus, \[h=r-r_E=42.176\times 10^6\space m-6.37\times 10^6\space m =35.806\times 10^6\space m=35806\space km= 22240\space mi\space(Answer)\]

6. [60] In Fig. 13-13, two satellites, A and B, both of mass m = 125 kg, move in the same circular orbit of radius \(r = 7.87 \times 10^6\) m around Earth but in opposite senses of rotation and therefore on a collision course.

1. Find the total mechanical energy \(E_A + E_B\) of the two satellites + Earth system before the collision.
2. If the collision is completely inelastic so that the wreckage remains as one piece of tangled material (mass = 2m), find the total mechanical energy immediately after the collision. (c) Just after the collision, is the wreckage falling directly toward Earth’s center or orbiting around Earth?

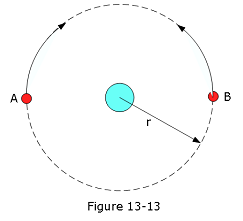
Solution:

1. Total mechanical energy of two satellites: \[E_A+E_B=-\frac{GMm}{2r}-\frac{GMm}{2r}=-\frac{GMm}{r} =-\frac{(6.67\times 10^{-11}\frac{m^3}{kg-s^2})(5.98\times 10^{24}\space kg)(125\space kg)}{7.8\times 10^6\space m} =-6.33\space 10^9\space J\]

2. After the inelastic collision, total mechanical energy is

\[E=-\frac{GM(2m)}{2r}=-6.33\space 10^9\space J\]

3. After the collision, no kinetic energy, so the wreckage will fall towards the center of Earth.

7. [61] (a) At what height above Earth’s surface is the energy required to lift a satellite to that height equal to the kinetic energy required for the satellite to be in orbit at that height? (b) For greater heights, which is greater, the energy for lifting or the kinetic energy for orbiting?

Solution: (a) To lift a satellite energy required \[U_i=-\frac{GMm}{r_E} ;U_f=-\frac{GMm}{r_E+h}\]

\[\Delta U = U_f-U_i=-\frac{GMm}{(r_E+h)}+\frac{GMm}{r_E}\]

Kinetic energy requires to put into circular orbit

\[K=\frac{GMm}{(r_E+h)}\]

Using \(\Delta U = K\)

\[-\frac{GMm}{(r_E+h)}+\frac{GMm}{r_E}=\frac{GMm}{2(r_E+h)}\]

\[\frac{1}{r_E}=\frac{3}{2(r_E+h)}\space or, 2(r_E+h) = 3r_E,\space h=\frac{r_E}{2}=3.19\times 10^6\space m(Answer)\]

2. Greater energy is required to lift to a greater height.

8. [66] One way to attack a satellite in Earth orbit is to launch a swarm of pellets in the same orbit as the satellite but in the opposite direction. Suppose a satellite in a circular orbit 500 km above Earth’s surface collides with a pellet having mass 4.0 g. (a) What is the kinetic energy of the pellet in the reference frame of the satellite just before the collision? (b)What is the ratio of this kinetic energy to the kinetic energy of a 4.0 g bullet from a modern army rifle with a muzzle speed of 950 m/s?

Solution

1. Kinetic energy is \[K= \frac{1}{2}mv^2=\frac{GMm}{2r}\]

\[K = \frac{1}{2}m(2v)^2=(\frac{1}{2}mv^2)4=4(\frac{GMm}{2r}) = \frac{2(6.67\times 10^{-11}\frac{m^3}{kg-s^2})(5.98\times 10^{24}\space kg)(4\times 10^-3\space kg)}{6370+500)\times 10^3\space m} =4.6\times 10^5\space J\space(Answer)\]

2. \[\frac{K}{K_B}=\frac{4.6\times 10^5\space J}{\frac{1}{2}(4.0\times 10^{-3}\space kg)(950\space m/s)^2} =254.85\space(Answer)\]

Problems:

Section 13-1 Newton’s Laws of Gravitation:

1. [4] The Sun and Earth each exert a gravitational force on the Moon. What is the ratio \(\frac{F_{Sun}}{F_{Earth}}\) of these two forces? (The average Sun–Moon distance is equal to the Sun–Earth distance.)

Section 13-2 Gravitation and the Principle of Superposition:

2. [8] In Fig. 13-34, three 5.00 kg spheres are located at distances \(d_1=0.300\) m and \(d_2=0.400\) m. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the net gravitational force on sphere B due to spheres A and C?

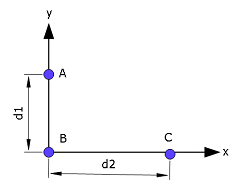
Solution: (a) \[F_{BA}=\frac{Gm_1m_2}{d_1^2}=\frac{(6.67\times 10^{-11}\frac{m^3}{kg-s^2})(5\space kg)^2}{0.300\space m)^2} =1.85\times 10^{-8}\space N\]

\[F_{BC}=\frac{Gm_1m_2}{d_2^2}=\frac{(6.67\times 10^{-11}\frac{m^3}{kg-s^2})(5\space kg)^2}{0.400\space m)^2} =1.04\times 10^{-8}\space N\]

Magnitude of the net gravitational force on B: \[F_{net}=\sqrt{F_{BA}^2+F_{BC}^2} =\sqrt{(1.85\times 10^{-8}\space N)^2+(1.04\times 10^{-8}\space N)^2}= 2.12\times 10^{-8}\space N\space(Answer)\]

2. Direction of the net gravitational force: \[\theta=tan^-1\frac{F_{BA}}{F_{BC}}= tan^{-1}\left(\frac{1.85\times 10^{-8}}{1.04\times 10^{-8}}\right) =60.66^\circ\space(Answer)\]

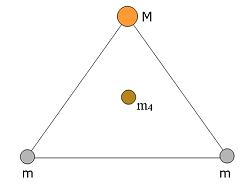
3. [11] As seen in Fig. 13-36, two spheres of mass m and a third sphere of mass M form an equilateral triangle, and a fourth sphere of mass m4 is at the center of the triangle. The net gravitational force on that central sphere from the three other spheres is zero. (a) What is M in terms of m? (b) If we double the value of \(m_4\), what then is the magnitude of the net gravitational force on the central sphere?

4. [25] A solid sphere has a uniformly distributed mass of \(1.0 \times 10^4\) kg and a radius of 1.0 m. What is the magnitude of the gravitational force due to the sphere on a particle of mass m when the particle is located at a distance of (a) 1.5 m and (b) 0.50 m from the center of the sphere? (c) Write a general expression for the magnitude of the gravitational force on the particle at a distance \(r \leq 1.0\) m from the center of the sphere.

Section 13-3 Gravitational Potential Energy:

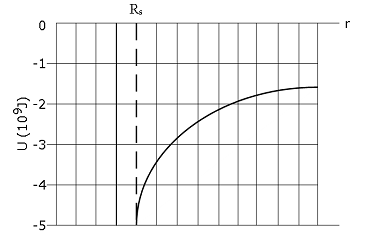
5. [29] Figure 13-43 gives the potential energy function U(r) of a projectile, plotted outward from the surface of a planet of radius \(R_s\). What least kinetic energy is required of a projectile launched at the surface if the projectile is to “escape” the planet?

Solution:

Maximum potential energy from Figure 13-43: \(U(r) = -5\times 10^9\space J\)

Kinetic energy: \[K = -U = -(-5\times 10^9\space J)=5\times 10^9\space J\space(Answer)\]

6. [33] What multiple of the energy needed to escape from Earth gives the energy needed to escape from

1. the Moon and (b) Jupiter?

Solution:

1. Kinetic energy needed to escape from Moon:

\(K_E=\frac{GM_Em}{R_E}\)

\(K_M=\frac{GM_Mm}{R_M}\)

\(\frac{K_M}{K_E}=\frac{M_M}{M_E}\frac{R_E}{R_M}=0.0451\)

2. Kinetic energy needed to escape from Jupiter:

\(K_E=\frac{GM_Em}{R_E}\)

\(K_J=\frac{GM_Jm}{R_J}\)

\(\frac{K_J}{K_E}=\frac{M_J}{M_E}\frac{R_E}{R_J}=28.96\)

7. [40] A projectile is shot directly away from Earth’s surface. Neglect the rotation of Earth. What multiple of Earth’s radius \(R_E\) gives the radial distance a projectile reaches if (a) its initial speed is 0.500 of the escape speed from Earth and (b) its initial kinetic energy is 0.500 of the kinetic energy required to escape Earth? (c) What is the least initial mechanical energy required at launch if the projectile is to escape Earth?

Section 13-3 Planets and Satellites: Kepler’s Laws

8. [43] (a) What linear speed must an Earth satellite have to be in a circular orbit at an altitude of 160 km above Earth’s surface? (b)What is the period of revolution?

9. [47] The Sun, which is \(2.2 \times 10^{20}\) m from the center of the Milky Way galaxy, revolves around that center once every \(2.5 \times 10^8\) years. Assuming each star in the Galaxy has a mass equal to the Sun’s mass of \(2.0 \times 10^{30}\) kg, the stars are distributed uniformly in a sphere about the galactic center, and the Sun is at the edge of that sphere, estimate the number of stars in the Galaxy.

10. [57] In a certain binary-star system, each star has the same mass as our Sun, and they revolve about their center of mass. The distance between them is the same as the distance between Earth and the Sun.What is their period of revolution in years?

Solution

Binary-star system has two identical stars, each star has the mass of Sun, which is \(1.00\times10^{30}\times kg\), revolve about their center of mass. The distance between the two stars is 1 AU = \(1.5\times 10^{11}\times m\). Gravitational force between the stars is \(F=\frac{GMM}{r^2}\).

\[\frac{GMM}{r^2}=\frac{Mv^2}{r/2}=\frac{2Mv^2}{r}$, where $v=\frac{2\pi(r/2)}{T}=\frac{\pi r}{T}\]

Therefore, \[\frac{GM}{r^2}=\frac{2\pi^2r}{T}\] \[T=\sqrt{\frac{2\pi^2r^3}{GM}} =\sqrt{\frac{2\pi^2(1.5\times 10^11\space m)^3}{(6.67\times 10^{-11}\frac{m^3}{kg-s^2})(1.5\times 10^{30}\space kg)}}=2.24\times 10^7\times s = \frac{2.24\times 10^7\times s}{3.154\times 10^7\space s}=0.71\space y\space(Answer)\]

Section 13-3 Satellites: Orbits and Energy

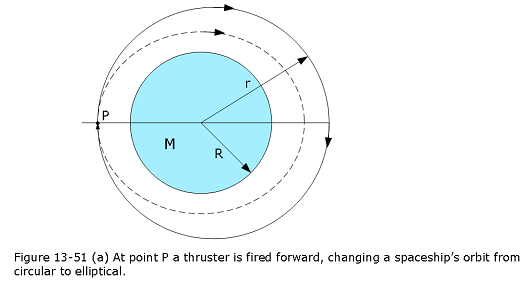
11. [68] Two small spaceships, each with mass m = 2000 kg, are in the circular Earth orbit of Fig. 13-51, at an altitude h of 400 km. Igor, the commander of one of the ships, arrives at any fixed point in the orbit 90 s ahead of Picard, the commander of the other ship. What are the (a) period \(T_0\) and (b) speed \(v_0\) of the ships? At point P in Fig. 13-51, Picard fires an instantaneous burst in the forward direction, reducing his ship’s speed by 1.00%. After this burst, he follows the elliptical orbit shown dashed in the figure. What are the

3. kinetic energy and (d) potential energy of his ship immediately after the burst? In Picard’s new elliptical orbit, what are (e) the total energy E, (f) the semimajor axis a, and (g) the orbital period T? (h) How much earlier than Igor will Picard return to P?