Chapter 16 Waves-II

Learning Objectives:

In this chapter you will basically learn:

\(\bullet\) Distinguish between a longitudinal wave and a transverse wave.

\(\bullet\) Apply the relationship between the speed of sound through a material, the material’s bulk modulus, and the material’s density.

\(\bullet\) Given a displacement function s(x, t) for a sound wave, calculate the time between two given displacements.

\(\bullet\) Apply the relationships between wave speed v, angular frequency \(\omega\), angular wave number k, wavelength \(\lambda\), period T, and frequency f.

\(\bullet\) For any particular time and position, calculate the pressure variation (variation from atmospheric pressure) of an element of air as a sound wave travels through its location.

\(\bullet\) Apply the relationship between pressure-variation amplitude \(\Delta P_m\) and displacement amplitude \(s_m\).

\(\bullet\) Given the phase difference between two sound waves with the same amplitude, wavelength, and travel direction, determine the type of interference between the waves (fully destructive interference, fully constructive interference, or indeterminate interference).

\(\bullet\) Convert a phase difference between radians, degrees, and number of wavelengths.

\(\bullet\) Calculate the sound intensity I at a surface as the ratio of the power P to the surface area A.

\(\bullet\) Apply the relationship between the sound intensity I and the displacement amplitude \(s_m\) of the sound wave.

\(\bullet\) Apply the relationship between the sound level \(\beta\), the sound intensity I, and the standard reference intensity \(I_0\).

\(\bullet\) Explain how beats are produced.

\(\bullet\) Identify that the Doppler effect is the shift in the detected frequency from the frequency emitted by a sound source due to the relative motion between the source and the detector.

\(\bullet\) Identify that in calculating the Doppler shift in sound, the speeds are measured relative to the medium (such as air or water), which may be moving.

\(\bullet\) Calculate the shift in sound frequency for (a) a source moving either directly toward or away from a stationary detector, (b) a detector moving either directly toward or away from a stationary source, and (c) both source and detector moving either directly toward each other or directly away from each other.

\(\bullet\) Sketch the bunching of wavefronts for a sound source traveling at the speed of sound or faster.

\(\bullet\) For a sound source exceeding the speed of sound, apply the relationship between the Mach cone angle, the speed of sound, and the speed of the source.

16.0.1 The importance of sound waves:

Five basic senses of humans are touch, sight, hearing, smell and taste. Humans can normally hear sound waves of frequencies between 20 and 20,000 Hz (20kHz). Sound frequencies above 20 kHz, are called ultrasonic or ultrasound wave. Humans cannot hear ultrasonic waves, but there are various technological tools such as sonar systems, sonograms, surgical tools, and cleaning sytems that are very useful for practical applications.

SONAR stands for Sound Navigation Ranging. Sonar have been used in navigation, forecasting weather, and for tracking aircraft, ships, submarines, and missiles. Sonar devices work similar to light waves by bouncing sound waves from objects to determine their location. A sonar system consisting of an ultrasonic transmitter and a receiver. The location of an object is determined from the time elapsed between the emission of the ultrasonic sound and the reception of its reflection off the objects. Ultrasound imaging is used in medical science to create two dimensional black-and-white image of organs and various parts of human body with sufficient accuracy.

The medical physiologists are yet to understand how speech is produced, how speech impairment might be corrected, how hearing loss can be alleviated, and even how snoring is produced. There are many kinds of acoustic dampers that are being used by acoustic engineers for reducing noise and improving the acoustics of cimema halls, cathedrals and concert halls. The shock waves produced by supersonic aircraft are of concern to aviation engineers in communities near an airport in terms of noise level as well as the failure of the civil structure due to resonance.

[Some medical researchers are concerned with how noises produced by the heart and lungs can signal a medical problem in a patient. Some paleontologists are concerned with how a dinosaur’s fossil might reveal the dinosaur’s vocalizations. Some military engineers are concerned with how the sounds of sniper fire might allow a soldier to pinpoint the sniper’s location, and, on the gentler side, some biologists are concerned with how a cat purrs.]

16.0.2 Sound Waves:

Sould waves are mechanical waves that require a material medium to propagate. There are two types of mechanical waves: Transverse waves involve oscillations perpendicular to the direction in which the wave travels; longitudinal waves involve oscillations parallel to the direction of wave travel.

In Chapter 15 Waves-I we derived an equation for the speed of a transverse wave along a stretched string and is given in Eq. 15-10 as \(v = \sqrt{\frac{\tau}{\mu}}=\sqrt{\frac{elastic~property}{intertial~property}}\),where (for transverse waves) \(\tau\) is the tension in the string and \(\mu\) is the string’s linear mass density.

In this chapter we will study sound waves which are longitudinal mechanical waves that can travel through solids, liquids, or gases. The speed v of a sound wave in a medium having bulk modulus \(B=-\frac{\Delta p}{\Delta V/V}\) and density \(\rho\) is

\[\begin{equation} v=\sqrt\frac{B}{\rho}~~~(speed ~of ~sound).. \tag{16.1} \end{equation}\]

The speed of sound in air at \(20 C^o\), the speed of sound is 343 m/s. The density of water is almost 1000 times greater than the density of air. However, the bulk modulus of water is more than 1000 times greater than that of air since water is much more incompressible than air. Table 16-1 shows speed of sound in various media.

Table 16-1 Speed of \(sound^a\)

Medium	Speed (m/s)
Gases
Air (\(0^0C)\)	331
Air (\(20^0C)\)	343
Helium	965
Hydrogen	1284
Liquids
Water (\(0^0C\))	1402
Water (\(20^0C\))	1482
Sea Water\(^b\)	1522
Solids
Aluminum	6420
Steel	5941
Granite	6000

\(^a\) At \(0^0\)C and 1 atm pressure, except where noted..

\(^b\) At \(20^0\)C and 3.5% salinity.

16.0.3 Traveling Sound Waves:

Figure 16-1 displays a wave traveling rightward through a long air-filled tube producing a wave by sinusoidally moving a piston at the left end of the tube. We examine the displacements and pressure variations associated with a sinusoidal sound wave traveling through air.

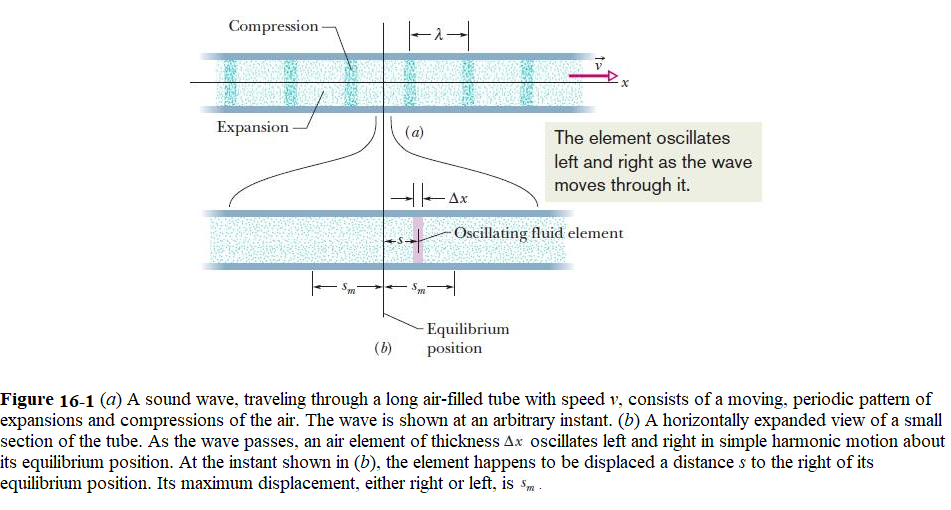
Displacement:

The displacements s(x, t) as shown in Fig. 16-1 are sinusoidal functions of x and t, as a cosine function, as

\[\begin{equation} s(x,t)=s_m\cos(kx-\omega t). \tag{16.2} \end{equation}\]

Figure 16-2a labels the various parts of the Eq. 16-2, \(s_m\) is the displacement amplitude—that is, the maximum displacement of the air element to either side of its equilibrium position (see Fig. 16-1b). The angular wave number k, angular frequency \(\omega\), frequency f, wavelength \(\lambda\), speed v, and period T for a sound (longitudinal) wave.

16.0.4 Pressure:

As the wave moves, the air pressure at any position x in Fig. 16-1a varies sinusoidally.To describe this variation we write

\[\begin{equation} \Delta p(x,t)=\Delta p_m\sin(kx-\omega t). \tag{16.3} \end{equation}\]

Figure 16-2b labels the Eq.16-3. A negative value of \(\Delta p\) in Eq. 16-3 corresponds to an expansion of the air, and a positive value to a compression. Here \(\Delta p_m\) is the pressure amplitude, which is the maximum increase or decrease in pressure due to the wave; \(\Delta p_m\) is normally very much less than the pressure p present when there is no wave.

Derivation of Eq. 16-3:

The pressure variation in the displaced element in Eq. 16-3,

\[\begin{equation} \Delta p=-B\frac{\Delta V}{V}. \tag{16.4} \end{equation}\]

The quantity V in Eq. 16-4 is the volume of the element, given by

\[\begin{equation} V = A\Delta x. \tag{16.5} \end{equation}\]

The quantity \(\Delta V\) in Eq. 16-4 is the change in volume that occurs when the element is displaced. This volume change comes about because the displacements of the two faces of the element are not quite the same, differing by some amount \(\Delta s\).Thus,we can write the change in volume as

\[\begin{equation} \Delta V = A\Delta s. \tag{16.6} \end{equation}\]

Substituting Eqs. 16-5 and 16-6 into Eq. 17-4 and passing to the differential limit yield

\[\begin{equation} \Delta p = -B\frac{\Delta s}{\Delta x}=-B\frac{\partial s}{\partial x}. \tag{16.7} \end{equation}\]

The symbols \(\partial\) indicate that the derivative in Eq. 16-7 is a partial derivative, which tells us how s changes with x when the time t is fixed. From Eq. 16-2 we then have, treating t as a constant,

\[\frac{\partial s}{\partial x}=\frac{\partial}{\partial x}\left[s_m\cos(kx-\omega t)\right]=-ks_m\sin(kx-\omega t).\]

Substituting this quantity for the partial derivative in Eq. 16-7 yields

\[\Delta p = Bks_m\sin(kx-\omega t).\]

This tells us that the pressure varies as a sinusoidal function of time and that the amplitude of the variation is equal to the terms in front of the sine function.

Setting \(\Delta p_m = Bks_m,\) \[\Delta p_m = Bks_m=(v^2\rho k)s_m\].

16.0.5 Interference of Waves:

Similar to transverse waves, two sound waves with the same amplitude and wavelength are moving in the positive direction of an x axis with a phase difference of \(\phi\) can interfere. Unlike sine functions in case of transverse waves, we use cosine functions to study the interference of sound waves:

\[\begin{equation} s_1(x,t) = s_m\cos(kx-\omega t), \end{equation}\]

and

\[\begin{equation} s_2(x,t) = s_m\cos(kx-\omega t+\phi). \end{equation}\]

Using the trigonometric identity in Appendix-A, we can add Eq. 16-8 and 16-9

\[\begin{equation} s'= s_m\cos(kx-\omega t)+s_m\cos(kx-\omega t+\phi)=\left[2s_m\cos\frac{1}{2}\phi\right]\cos(kx-\omega t+\frac{1}{2}\phi). \end{equation}\]

The resultant wave is a traveling wave with amplitude of the magnitude is given by

\[\begin{equation} s_m' = |2s_m\cos\frac{1}{2}\phi|. \tag{16.8} \end{equation}\]

The value of \(\phi\) determines the interference and can be related to phase difference \(\phi\) to path length difference \(\Delta L\), that a phase difference of \(2\pi\) rad corresponds to one wavelength. Thus,we can write the proportion.

\[\begin{equation} \frac{\phi}{2\pi}=\frac{\Delta L}{\lambda}. \tag{16.9} \end{equation}\]

where \(\Delta |L=L_2-L_1|\) is the path length difference as shown in Fig. 16-3.

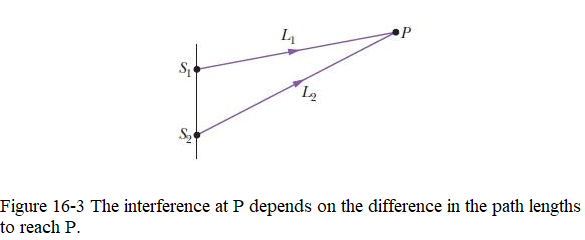
From Eq. 16-9, we get

\[\begin{equation} \phi=\frac{\Delta L}{\lambda}2\pi. \tag{16.10} \end{equation}\]

Fully constructive interference occurs when \(\phi\) is zero, \(2\pi\), or any integer multipl of \(2\pi\). We can write this condition as

\[\begin{equation} \phi= m(2\pi), for~ m~ = 0,1,2,..... (fully~ constructive ~interference). \tag{16.11} \end{equation}\]

From Eq. 16-10, this occurs when the ratio \(\frac{\Delta L}{\lambda}\) is

\[\begin{equation} \frac{\Delta L}{\lambda} = 0,1,2,..... (fully~ constructive ~interference). \tag{16.12} \end{equation}\]

Fully destructive interference occurs when f is an odd multiple of \(\pi\):

\[\begin{equation} \phi = (2m+1)\pi, for ~~m= 0,1,2,..... (fully~ destructive ~interference). \tag{16.13} \end{equation}\]

From Eq. 16-10, this occurs when the ratio \(\frac{\Delta L}{\lambda}\) is

\[\begin{equation} \frac{\Delta L}{\lambda} = 0.5,1.5,2.5,.. (fully~ destructive ~interference). \tag{16.14} \end{equation}\]

16.0.6 Intensity and Sound Level:

The loudness of sound is different than the frequency, wavelength, and speed. Loudness of a sound is due to the intensity I of a sound wave at a surface is the average rate per unit area at which energy is transferred by the wave through or onto the surface. We can write this as

\[\begin{equation} I = \frac{P}{A}, \tag{16.15} \end{equation}\]

where P is the time rate of energy transfer (the power) of the sound wave and A is the area of the surface intercepting the sound.

Consider, in Fig. 16-1a, a thin slice of air of thickness dx, area A, and mass dm, oscillating back and forth as the sound wave of Eq. 16-2 passes through it. The kinetic energy dK of the slice of air is

\[\begin{equation} dK = \frac{1}{2}dm~v_s^2, \tag{16.16} \end{equation}\]

where \(v_s\) is not the speed of the wave but the speed of the oscillating element of air, obtained from Eq. 16-2 as

\[\begin{equation} v_s = \frac{\partial s}{\partial t} = -\omega s_m\sin(kx-\omega t). \end{equation}\]

Substituting \(dm = \rho A~dx\), eq.16-16 can be written as

\[\begin{equation} dK = \frac{1}{2}(\rho A~dx)~(-\omega s_m)^2\sin^2(kx-\omega t). \tag{16.17} \end{equation}\]

Dividing Eq. 16-17 by \(dt\)gives the rate at which kinetic energy moves along with the wave, and using for transverse waves, \(v=\frac{dx}{dt}\) is the wave speed v, we have

\[\begin{equation} \frac{dK}{dt} = \frac{1}{2}\rho A~v~\omega^2 s_m^2\sin^2(kx-\omega t). \tag{16.18} \end{equation}\]

The average rate at which kinetic energy is transported is the average value of the square of a sine (or a cosine) function over one full oscillation is \(\frac{1}{2}\).Thus,

\[\begin{equation} \frac{dK}{dt}_{avg} = \frac{1}{2}\rho A~v~\omega^2 s_m^2\left[\sin^2(kx-\omega t)\right]_{avg}=\frac{1}{4}\rho A~v~\omega^2 s_m^2. \tag{16.19} \end{equation}\]

Assuming that the potential energy is carried along with the wave with the same rate as the rate of kinetic energy. The wave intensity I, which is the average rate per unit area at which energy of both kinds is transmitted by the wave, is then, from Eq. 16-19,

\[\begin{equation} I = \frac{2(dK/dt)_{avg}}{A} = \frac{1}{2}\rho~v~\omega^2~s_m^2. \tag{16.20} \end{equation}\]

16.0.7 The Decibel Scale:

The displacement amplitude at the human ear ranges from about \(10^{-5}\) m for the loudest tolerable sound to about \(10^{-11}\) m for the faintest detectable sound, a ratio of \(10^6\). Thus, instead of speaking of the intensity I of a sound wave, it is much more convenient to speak of its sound level \(\beta\) defined as

begin{equation} = (10~dB)LOG. \tag{16.21} \end{equation}

Here dB is the abbreviation for decibel, the unit of sound level, a name that was chosen to recognize the work of Alexander Graham Bell. \(I_0\) in Eq. 16-21 is a standard reference intensity \((10^{-12} W/m^2)\), chosen because it is near the lower limit of the human range of hearing. For \(I = I_0\), Eq. 16-21 gives \(\beta = 10~log~1=0\), so our standard reference level corresponds to zero decibels. Then \(\beta\) increases by 10 dB every time the sound intensity increases by an order of magnitude (a factor of 10). Table 17-2 lists the sound levels for a variety of environments.

Table 16-2 Some Sound Levels (dB)

Sources of Sound	dB
Hearing threshold	0
Rustle of leaves	10
Conversation	60
Washing machine, dishwasher	70
Motorcycle	95
Pain threshold	120
Jet engine	130
Firecrackers	140-150

16.0.8 Sources of Musical Sound:

The simplest standing wave pattern that can be set up in a pipe with two open ends also sound wave patterns that can be set up in a pipe with only one open end.Figure 16-4 shows standing wave patterns for string waves superimposed on pipes to represent standing sound wave patterns in the pipes. (a) With both ends of the pipe open, any harmonic can be set up in the pipe. (b) With only one end open, only odd harmonics can be set up.

More generally, the resonant frequencies for a pipe of length L with two open ends correspond to the wavelengths

\[\begin{equation} \lambda=\frac{2L}{n},~~~for~~~n=1,2,3,....... \tag{16.22} \end{equation}\]

where n is called the harmonic number. Letting v be the speed of sound, we write the resonant frequencies for a pipe with two open ends as

\[\begin{equation} f=\frac{v}{\lambda}=\frac{nv}{2L},~~~for~~~n=1,2,3,....(pipe,~ two~ open~ ends). \tag{16.23} \end{equation}\]

More generally, the resonant frequencies for a pipe of length L with one open end correspond to the wavelengths

\[\begin{equation} \lambda=\frac{4L}{n},~~~for~~~n=1,3,5,....... \tag{16.24} \end{equation}\]

where n is called the harmonic number. Letting v be the speed of sound, we write the resonant frequencies for a pipe with one open end as

\[\begin{equation} f=\frac{v}{\lambda}=\frac{nv}{4L},~~~for~~~n=1,3,5,....(pipe,~ one~ open~ end). \tag{16.25} \end{equation}\]

16.0.9 Beats:

If two sounds reach our ears simultaneously, whose frequencies are very close to each other we cannot distinguish their difference. We also hear a striking variation in the intensity of this sound—it increases and decreases in slow, wavering beats that repeat at a frequency, the difference between the two combining frequencies. Figure 17-18 shows this beat phenomenon.

Let the time-dependent variations of the displacements due to two sound waves of equal amplitude \(s_m\) be

\[\begin{equation} s_1 = s_m\cos\omega_1 t ~and~ s_2 = s_m\cos\omega_2 t \tag{16.26} \end{equation}\]

where \(\omega_1 \gg \omega_2\). From the superposition principle, the resultant displacement is the sum of the individual displacements:

\[\begin{equation} s = s_1+s_2=s_m(\cos\omega_1 t + \cos\omega_2 t). \tag{16.27} \end{equation}\]

Using the following trigonometric identity as given in Appendix A

\[\begin{equation} \cos\alpha+\cos\beta=2\cos\frac{1}{2}(\alpha+\beta)\cos\frac{1}{2}(\alpha-\beta) \end{equation}\]

the resultant displacement as

\[\begin{equation} s=2s_m\cos\left[\frac{1}{2}(\omega_1-\omega_2)t\right] \cos\left[\frac{1}{2}(\omega_1 + \omega_2)t\right]. \tag{16.28} \end{equation}\]

Let’s assume

\[\begin{equation} \omega'=\frac{1}{2}(\omega_1-\omega_2)~~and~~\omega=\frac{1}{2}(\omega_1+\omega_2). \tag{16.29} \end{equation}\]

Now using the Eq. 16-29 in Eq. 16-28, we get

\[\begin{equation} s(t)=\left[2s_m\cos\omega' t\right]\cos\omega t. \tag{16.30} \end{equation}\]

Assuming that the angular frequencies \(\omega_1\) and \(\omega_2\) are almost equal, which means that \(\omega \gg \omega'\), in Eq. 16-29. We can then regard Eq. 16-30 as a cosine function whose angular frequency is \(\omega\) and whose amplitude (which is not constant but varies with angular frequency \(\omega'\)) is the absolute value of the quantity in the brackets.

A maximum amplitude will occur whenever \(\cos\omega't\) in Eq. 16-30 has the value +1 or -1, which happens twice in each repetition of the cosine function. Because \(\cos\omega't\) has angular frequency \(\omega'\), the angular frequency \(\omega_{beat}\) at which beats occur is \(\omega_{beat}=2\omega'\). Then, with the aid of Eq. 16-29, we can write the beat angular frequency as

\[\begin{equation} \omega_{beat}=2\omega'=2\frac{1}{2}(\omega_1-\omega_2)=\omega_1-\omega_2. \end{equation}\]

Using \(\omega = 2\pi f\) we get

\[\begin{equation} f_{beat}=f_1-f_2~~~~~(beat ~frequency). \tag{16.31} \end{equation}\]

Musicians use the beat phenomenon in tuning instruments. If an instrument is sounded against a standard frequency (for example, the note called “concert A” played on an orchestra’s first oboe) and tuned until the beat disappears, the instrument is in tune with that standard. In musical Vienna, concert A (440 Hz) is available as a convenient telephone service for the city’s many musicians.

16.0.10 Doppler Effect:

These motion-related frequency changes are due to the Doppler effect. The Doppler effect holds not only for sound waves but also for electromagnetic waves, including microwaves, radio waves, and visible light. Here, however, we shall consider only sound waves, and we shall take as a reference frame the body of air through which these waves travel.

The general equation holding for either the detector or the source is moving, or both are moving, the emitted frequency f and the detected frequency f’ are related by

\[\begin{equation} f'=f\frac{v\pm v_D}{v\pm v_S}~~~(general~equation~of~Doppler~effect), \tag{16.32} \end{equation}\]

where v is the speed of sound through the air, \(v_D\) is the detector’s speed relative to the air, and \(v_S\) is the source’s speed relative to the air. The choice of plus or minus signs is set by this rule:

When the motion of detector or source is toward the other, the sign on its speed must give an upward shift in frequency.When the motion of detector or source is away from the other, the sign on its speed must give a downward shift in frequency.

In short, toward means shift up, and away means shift down.

Here are some examples of the rule. If the detector moves toward the source, use the plus sign in the numerator of Eq. 16-32 to get a shift up in the frequency. If it moves away, use the minus sign in the numerator to get a shift down. If it is stationary, substitute 0 for \(v_D\). If the source moves toward the detector, use the minus sign in the denominator of Eq. 16-32 to get a shift up in the frequency. If it moves away, use the plus sign in the denominator to get a shift down. If the source is stationary, substitute 0 for \(v_S\).

Next, we derive equations for the Doppler effect for the following two specific situations and then derive Eq. 16-32 for the general situation.

1. When the detector moves relative to the air and the source is stationary relative to the air, the motion changes the frequency at which the detector intercepts wavefronts and thus changes the detected frequency of the sound wave.

2. When the source moves relative to the air and the detector is stationary relative to the air, the motion changes the wavelength of the sound wave and thus changes the detected frequency (recall that frequency is related to wavelength).

16.0.11 Detector Moving, Source Stationary:

\[\begin{equation} f'=f\frac{v + v_D}{v}~~~(detector~ moving~toward~the~ stationary~source). \tag{16.33} \end{equation}\]

\[\begin{equation} f'=f\frac{v - v_D}{v}~~~(detector~ moving~away~from~the~ stationary~source). \tag{16.34} \end{equation}\]

16.0.12 Source Moving, Detector Stationary:

\[\begin{equation} f'=f\frac{v}{v - v_S}~~~(source~ moving~toward~the~ stationary~detector). \tag{16.35} \end{equation}\]

\[\begin{equation} f'=f\frac{v}{v + v_S}~~~(source~ moving~away~from~the~ stationary~detector). \tag{16.36} \end{equation}\]

Supersonic Speeds, Shock Waves:

If a source is moving toward a stationary detector at a speed \(v_S\) equal to the speed of sound v, Eq. 16-35 predicts that the detected frequency f’ will be infinitely great.This means that the source is moving so fast that it keeps pace with its own spherical wavefronts (Fig. 16-5a). What happens when \(v_S > v\)? For such supersonic speeds, Eq. 16-35 no longer apply. Figure 16-5b depicts the spherical wavefronts that originated at various positions of the source.The radius of any wavefront is vt, where t is the time that has elapsed since the source emitted that wavefront. Note that all the wavefronts bunch along a V-shaped envelope in this two-dimensional drawing. The wavefronts actually extend in three dimensions, and the bunching actually forms a cone called the Mach cone. A shock wave exists along the surface of this cone, because the bunching of wavefronts causes an abrupt rise and fall of air pressure as the surface passes through any point.

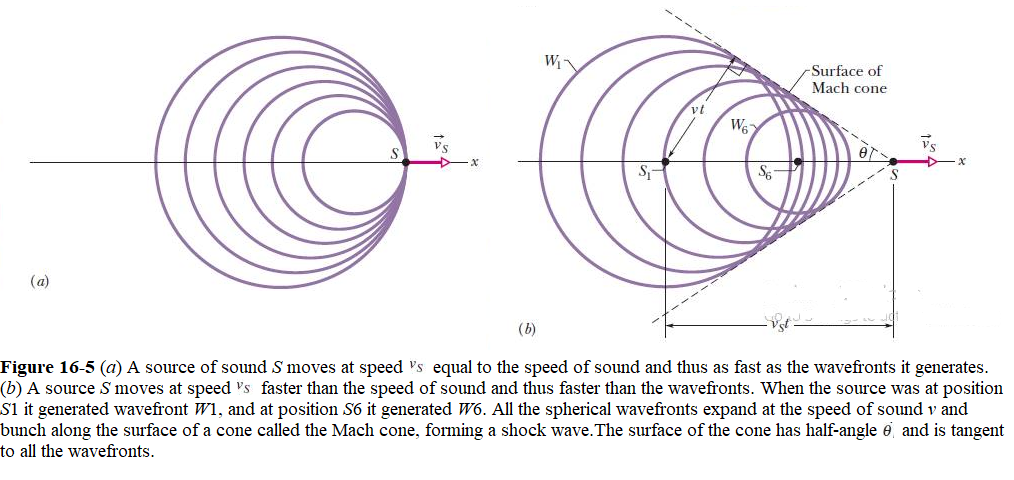
From Fig. 16-5b, we see that the half-angle u of the cone (the Mach cone angle) is given by (Mach cone angle).

\[\begin{equation} \sin\theta=\frac{vt}{v_St}=\frac{v}{v_S}~~~(Mach~ cone~ angle). \tag{16.37} \end{equation}\]

The ratio \(v_S/v\) is the Mach number. If a plane flies at Mach 2.3, its speed is 2.3 times the speed of sound in the air through which the plane is flying. The shock wave generated by a supersonic aircraft (Fig. 16-6) or projectile produces a burst of sound, called a sonic boom, in which the air pressure first suddenly increases and then suddenly decreases below normal before returning to normal. Part of the sound that is heard when a rifle is fired is the sonic boom produced by the bullet. When a long bull whip is snapped, its tip is moving faster than sound and produces a small sonic boom—the crack of the whip.

(Solved Problems : 9, 11,12, 21,24, 27, 29, 43, 53, 59, 68)