Chapter 1 Measurement:
Learning Objectives:
In this chapter you will basically learn:
\(\bullet\) Learn the seven base quantities in the SI system.
\(\bullet\) Learn most frequently used prefixes for SI units.
\(\bullet\) Learn chain-link conversions to change units (here for length, area, and volume).
\(\bullet\) Learn to change units for time and mass by using chain-link conversions.
1.1 Seven SI Base Units:
Table 1-1 shows the units for the seven base quantities—length, mass, time, electric current, thermodynamic temperature, amount of substance and luminous intensity.
Table 1-1 Seven SI Base Units
| Quantity | Name | Symbol |
|---|---|---|
| length | meter | m |
| mass | kilogram | kg |
| time | second | s |
| electric current | ampere | A |
| thermodynamic temperature | kelvin | K |
| amount of substance | mole | mol |
| luminous intensity | candela | cd |
Two base units mole and candela need more explanations for better understanding by the students.
Instead of specifying the mass in conventional unit in kg it is the most convenient to express the amount of a substance in mole (mol), where
1 mol = \(6.02 \times 10^{23}\) elementary units
of any substance. Thus 1 mol of copper means \(6.02 \times 10^{23}\) atoms (the atom is the elementary unit), and 1 mol of copper oxide means \(6.02 \times 10^{23}\) molecules (the molecule is the elementary unit of the compound).
One mole of a substance contains \(N_A\) (Avogadro’s number) elementary units (usually atoms or molecules), where \(N_A\) is found experimentally to be \(N_A = 6.02 \times 10^{23}~ mol^-1\) (Avogadro’s number).
One molar mass M of any substance is the mass of one mole of the substance.
A mole is related to the mass m of the individual molecules of the substance by
\[\begin{equation} M = mN_A \tag{1.1} \end{equation}\]
The number of moles n contained in a sample of mass \(M_{sam}\), consisting of N molecules, is related to the molar mass M of the molecules and to Avogadro’s number \(N_A\) as given by
\[\begin{equation} n=\frac{N}{N_A}=\frac{M_{sam}}{M}=\frac{M_{sam}}{mN_A} \tag{1.2} \end{equation}\]
Sample Problem 1-1 Avogadro’s Number
Find the mass in kilograms of \(7.50 \times 10^{24}\) atoms of arsenic, which has a molar mass of 74.9 g/mol.
Given molar mass M = \(74.9 \times 10^{-3} kg/mol\) and number of arsenic atom N = \(7.50 \times 10^{24}\).
Using Eq. 1-2, we get
\[M_{sam}=\frac{NM}{N_A}=\frac{(7.50 \times 10^{24})(74.9 \times 10^{-3} kg/mol)}{6.02 \times 10^{23}/mole}=0.933~kg~(Answer)\]
Sample Problem 1-2 Avogadro’s Number
Gold has a molar mass of 197 g/mol. (a) How many moles of gold are in a 2.50 g sample of pure gold? (b) How many atoms are in the sample?
- Given molar mass of gold M = 197 g/mol and \(M_{sam}=2.50 g\), using Eq. 1-2, the number of moles of gold is
\[n=\frac{M_{sam}}{M}=\frac{2.50~g}{197~g/mol}=0.01269~mol~(Answer)\]
- Again, using Eq. 1-2, the number of atoms in the sample using the result of (a) is
\[N = nN_A = (0.01269)\times (6.02\times 10^{23}=0.0763938\times 10^{23}~(Answer)\] Candela, Lumen, Lux: the equations Light is measured with different techniques, and also there are different units of measurements.
To understand candela one must understand the solid angle steradian. A solid angle in steradians is the ratio of \[\Omega=\frac{A}{r^2}.\] where A is the spherical surface area and r is the radius of the considered sphere as shown in Figure 1-1.
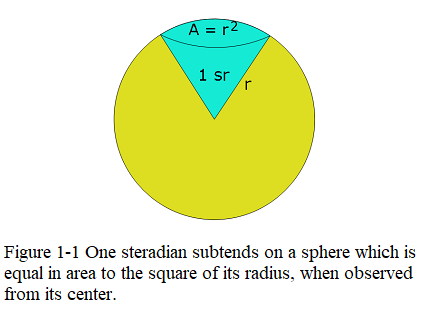
The solid angle of a sphere measured from any point in its interior is \(4\pi\) sr. One steradian is defined to be the solid angle subtended by a sphere with surface area \(A =r^2\).
The candela (cd) is the base unit of luminous intensity in the International System of Units (SI), which is the luminous power per unit solid angle or steradian emitted by a point light source in a particular direction.
Specifically, the candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency \(540\times 10^{12}\) hertz (540 THz) and that has a radiant intensity in that direction of 1/683 watt per steradian. The candela is abbreviated “cd.”
The lumen is defined as 1 cd sterradian, and the lux is defined as 1 cd sterradian \(m^{-2}\).
Converting Between Candelas and Lumens:
The candela vs. lumens, you cannot convert one to the other directly, as they do not represent the same physical thing. You can, however, work with the two at the same time and draw comparisons.
\[1~lm = cd\times 2\pi\left(1-cos\left(\frac{\alpha}{2}\right)\right)=cd\times \Omega\]
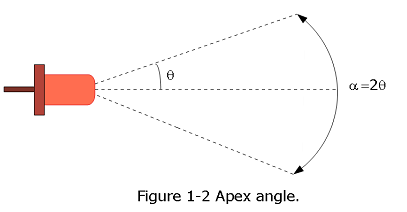
where, \(\alpha\) represents the cone apex angle and \(\Omega = 2\pi\left(1-cos\left(\frac{\alpha}{2}\right)\right)\).
One measures the angle between the axis where the light source gives its highest luminous intensity and the axis where that intensity is reduced to 50%. In the Figure 1-2, this angle is denoted with \(\theta\). The apex angle is twice that angle \(\alpha = 2\theta\).
Sample Problem 1-3 Candela
A point light source radiating equally in all directions, which is what is being considered here. Since the maximum value of \(\left(1-cos\left(\frac{\alpha}{2}\right)\right)\) is 2, which occurs when cos( = −1,
1 lm = 2\(\pi\)(1−(−1))cd = 4\(\pi\)cd
Thus for an isotopic sphere, lumens is just candelas times \(4\pi\).
1.2 Base Units and Derived Units:
Many SI derived units are defined in terms of seven base units. For example, the SI unit for power, called the watt (W), is defined in terms of the base units for mass, length, and time.
1 watt = 1 W = 1 J/s = 1 N-m/s = \(1 kg-m^{2}/s^{3}\)
where the last collection of unit symbols is read as kilogram-meter squared per second cubed.
1.3 Changing Units
We often need to change the units in which a physical quantity is expressed.We do so by a method called chain-link conversion. In this method, we multiply the original measurement by a conversion factor (a ratio of units that is equal to unity). For example, because 1 min and 60 s are identical time intervals, we have
\(\frac{1\space min}{60\space s}\) = 1 = \(\frac{60\space s}{1\space min}\)
\(2\space min = (2\space min)\times (1)= (2\space min)\frac{(60 s)\space}{(1\space min)}=120\space s\)
1.4 Prefix
When dealing with very large or very small measurements, we use the prefixes listed in Table 1-2. Each prefix represents a certain power of 10, to be used as a multiplication factor. Attaching a prefix to an SI unit has the effect of multiplying by the associated factor.
concat(’<!DOCTYPE html>Table 1-2 Prefixes for SI Units
| Factor | \(Prefix^a\) | Symbol |
|---|---|---|
| \(10^{24}\) | yotta- | Y |
| \(10^{21}\) | zetta- | Z |
| \(10^{18}\) | exa- | E |
| \(10^{15}\) | peta- | P |
| \(10^{12}\) | tera- | T |
| \(10^{9}\) | giga- | G |
| \(10^{6}\) | mega- | M |
| \(10^{3}\) | kilo- | k |
| \(10^{2}\) | hecto- | h |
| \(10^{1}\) | deka- | da |
| \(10^{-1}\) | deci- | d |
| \(10^{-2}\) | centi- | c |
| \(10^{-3}\) | milli- | m |
| \(10^{-6}\) | micro- | \(\mu\) |
| \(10^{-9}\) | nano- | n |
| \(10^{-12}\) | pico- | p |
| \(10^{-15}\) | femto- | f |
| \(10^{-18}\) | atto- | a |
| \(10^{-21}\) | zepto- | z |
| \(10^{-24}\) | yocto- | y |
’)
\(^aThe~ most~ frequently~ used~ prefixes~ are~ shown~ in~italic~type.\)
As an example of using prefix Giga (G):
\(1.27\space \times 10^{9}\space watts=1.27\space gigawatts=1.27\space GW\)
or a particular time interval as
\(2.35\space \times 10^{-9}\space s=2.35\space nanoseconds =2.35\space ns\)
1.5 Significant Figures and Decimal Places
Don’t confuse significant figures with decimal places. Consider the lengths 35.6 mm, 3.56 m, and 0.00356 m. They all have three significant figures but they have one, two, and five decimal places, respectively.
When the leftmost of the digits to be discarded is 5 or more, the last remaining digit is rounded up; otherwise it is retained as is. For example, 11.3516 is rounded to three significant figures as 11.4 and 11.3279 is rounded to three significant figures as 11.3.
1.6 A Second Mass Standard
It is the carbon-12 atom, which, by international agreement, has been assigned a mass of 12 atomic mass units (u).The relation between the two units is
\[\begin{equation} 1\space u = 1.66053886\times10^{-27}\space kg \tag{1.3} \end{equation}\]
with an uncertainty of \(\pm 10\) in the last two decimal places.
Solved Problems Measurement:
- [3] The micrometer (1 \(~\mu m\)) is often called the micron. (a) How many microns make up 1.0 km? (b) What fraction of a centimeter equals 1.0 \(~\mu m\)? (c) How many microns are in 1.0 yd?
1.0 km = (1.0 km)\(\left(\frac{1000\space m}{1\space km}\right)\left(\frac{1\space \mu m}{10^{-6}\space m}\right)=10^9\space \mu m\)
1.0 \(~\mu m\)=\(\left(\frac{10^{-6}\space m}{1\mu\space m}\right)\left(\frac{100\space cm}{1\space m}\right)=10^{-4}\space cm\)
1.0 yd = \((1.0\space yd)\left(\frac{3\space feet}{1\space yd}\right)\left(\frac {12\space inch}{1\space ft}\right)\left(\frac {2.54\space cm}{1\space in}\right)\left(\frac {10^{-2}\space m}{1\space cm}\right)\left(\frac {1\space\mu m}{1\space\times 10^{-6}\space m}\right)=9.1\times10^4\space\mu m\)
- [9] Antarctica is roughly semicircular, with a radius of 2000 km (Fig. 1-3). The average thickness of its ice cover is 3000 m. How many cubic centimeters of ice does Antarctica contain? (Ignore the curvature of Earth.)
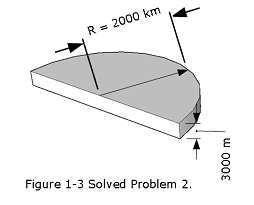
Solution:
\[Volume \space of\space ice\space contain\space in\space Antarctica: V =\left(\frac{\pi r^2}{2}\right )h\] \[r = (2000\space km)(\frac{1000\space m}{1\space km})(\frac {100\space cm}{1\space m})=2.0\times 10^8\space cm\] \[h=(3000\space m)(\frac{100\space cm}{1\space m})=3.0\times 10^5\space cm\]
\[V=\frac{\pi}{2}(2.0\times 10^8\space cm)^2(3.0\times 10^5\space cm)\approx 18.85\times 10^{21}\space cm^3\space(Answer)\]
- [13] Three digital clocks A, B, and C run at different rates anddo not have simultaneous readings of zero. Figure 1-4 shows simultaneous readings on pairs of the clocks for four occasions. (At the earliest occasion, for example, B reads 25.0 s and C reads 92.0 s.) If two events are 600 s apart on clock A, how far apart are they on (a) clock B and (b) clock C? (c) When clock A reads 400 s, what does clock B read? (d) When clock C reads 15.0 s, what does clock B read? (Assume negative readings for prezero times.)

- Comparing clock-A and clock-B with their respective matching points we get, slope of the two straight line points
\(m=\frac{290-125}{512-312}=\frac{165}{200}\)
Using the value of m and given the two events in clock-A to be 600 s apart the clock-B will read
\(m(600\space s) = \frac{165}{200}(600 \space s)\) = 495 s (Answer)
- Similarly, comparing clock-B and clock-C with their respective matching points we get, slope of the two straight line points
\(m = \frac{142-192}{200-25}=-\frac{2}{7}\)
Now since we found 495 s in clock-B, we get in clock-C,
\(\frac{2}{7}(495)=141.43\space s\)
- When clock-A reads 400 s, assume clock-B read some unknown U, i.e.,
\(\frac{512-400}{400-312}=\frac{290-U}{U-125}\), or U = 197.6 s
- Similar to (c), we get
\(\frac{U-200}{U-25}=\frac{15-142}{15-192}\), or U = -245 s
- [14] A lecture period (50 min) is close to 1 microcentury. (a) How long is a microcentury in minutes? (b) Using \[percentage ~difference = \left(\frac{actual-approximation}{actual}\right)\times 100\] find the percentage difference from the approximation.
\(1\space \mu century=(10^{-6}\space century)(\frac{100\space yrs}{1\space century})(\frac{365\space dys}{1\space yr})(\frac{24\space hrs}{1\space dy})(\frac{60\space min}{1\space hr})\approx 52.56\space mins\)
\(percentage ~difference = \left(\frac{actual-approximation}{actual}\right)\times 100=\left(\frac{52.56\space mins-50\space mins}{52.56\space mins}\right)\times 100=4.87\%\)
- [19] Suppose that, while lying on a beach near the equator watching the Sun set over a calm ocean, you start a stopwatch just as the top of the Sun disappears. You then stand, elevating your eyes by a height H = 1.70 m, and stop the watch when the top of the Sun again disappears. If the elapsed time is t = 11.1 s, what is the radius r of Earth?
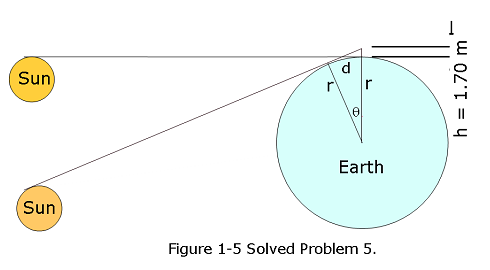
Applying Pythagorian law in the above figure we get:
\[(r+h)^2=d^2+r^2\] \[2rh+h^2=d^2\]
Since, the radius of Earth \(r\gg h\), we can write \[d^2\approx 2rh\]
Applying Pythagorian law \[tan\theta=\frac{d}{r}\], we get \[r^2 tan^2\theta \approx 2rh\]
In an elapsed time of t = 11.1 s, Earth rotates
\[\theta = \frac {306^{\circ}}{86400\space s}(11.1\space s)=0.04625^{\circ}\]
Therefore, the radius of the Earth can be approximately calculated to be
\[r\approx \frac{2h}{tan^2{\theta}}=\frac{2\times 1.70\space m}{tan^2(0.04625^\circ)}\approx 5.22\times 10^6\space m\space (Answer)\]
- [21] Earth has a mass of \(5.98 \times 10^{24}\) kg.The average mass of the atoms that make up Earth is 40 u. How many atoms are there in Earth?
Using Eq. 1-3, we find
1 u = \(1.66053886\times 10^{-27}kg\) \[40\space u = 40\times 1.66053886\times 10^{-27}kg \approx 66.42\times 10^{-27}kg\]
Numer of atoms in Earth is: \[\frac{5.98 \times 10^{24}}{66.42\times 10^{-27}kg}\approx 9.00\times 10^{49}\space atoms\]
- [53] An astronomical unit (AU) is equal to the average distance from Earth to the Sun, about \(92.9 \times 10^6 ~mi\). A parsec (pc) is the distance at which a length of 1 AU would subtend an angle of exactly 1 second of arc (Fig. 1-6). A light-year (ly) is the distance that light, traveling through a vacuum with a speed of 186000 mi/s, would cover in 1.0 year. Express the Earth – Sun distance in (a) parsecs and (b) light-years.
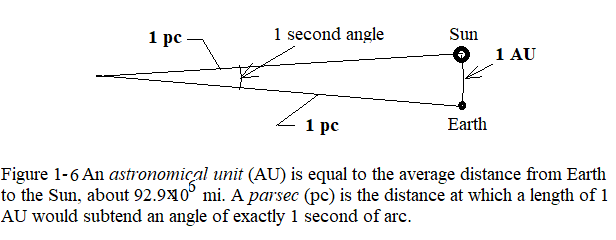
Using Figure 1-6, we can find a formula to express 1 AU in terms of pc, that is \[s=r\theta\]. First we need to convert \(\theta=1s\) either in degress or in radians as follows: \[\theta=1s=(1s)(\frac{1min}{60s})(\frac{1 deg}{60 min})(\frac{2\pi}{360 deg})=4.85\times\times 10^{-6} rad\] Therefore, \[1AU=s=r\theta=(1 pc)(4.85\times 10^{-6}rad)=4.85\times 10^{-6}pc (Answer)\]
Using\(~s = vt~\)formula, we can convert 1 ly to mile as follows: \[1 ly = (186000 mi/s)(365 \times 24 \times 60 \times 60 s)=5.87\times 10^{12}mi\]
\[1 AU = 92.9\times 10^6 mi=(92.9\times 10^6 mi)(\frac{1 ly}{5.87\times 10^{12}}mi)=1.57\times 10^{-5}ly(Answer)\]
Problems Measurement:
Section 1-1 Lengths
- [1] Earth is approximately a sphere of radius \(6.37 \times 10^6 m\). What are (a) its circumference in kilometers, (b) its surface area in square kilometers, and (c) its volume in cubic kilometers?
- [5] Horses are to race over a certain English meadow for a distance of 4.0 furlongs. What is the race distance in (a) rods and (b) chains? (1 furlong = 201.168 m, 1 rod = 5.0292 m, and 1 chain = 20.117 m.)
Section 1-2 Time
[11] For about 10 years after the French Revolution, the French government attempted to base measures of time on multiples of ten: One week consisted of 10 days, one day consisted of 10 hours, one hour consisted of 100 minutes, and one minute consisted of 100 seconds.What are the ratios of (a) the French decimal week to the standard week and (b) the French decimal second to the standard second?
[16] Time standards are now based on atomic clocks.A promising second standard is based on pulsars, which are rotating neutron stars (highly compact stars consisting only of neutrons). Some rotate at a rate that is highly stable, sending out a radio beacon that sweeps briefly across Earth once with each rotation, like a lighthouse beacon. Pulsar PSR 1937 + 21 is an example; it rotates once every 1.557 806 448 872 75 \(\pm\) 3 ms, where the trailing \(\pm\) 3 indicates the uncertainty in the last decimal place (it does not mean \(\pm\) 3 ms). (a) How many rotations does PSR 1937 + 21 make in 7.00 days? (b) How much time does the pulsar take to rotate exactly one million times and (c) what is the associated uncertainty?
[18] Because Earth’s rotation is gradually slowing, the length of each day increases:The day at the end of 1.0 century is 1.0 ms longer than the day at the start of the century. In 20 centuries, what is the total of the daily increases in time?
Section 1-3 Mass
[20] The record for the largest glass bottle was set in 1992 by a team in Millville, New Jersey—they blew a bottle with a volume of 193 U.S. fluid gallons. (a) How much short of 1.0 million cubic centimeters is that? (b) If the bottle were filled with water at the leisurely rate of 1.8 g/min, how long would the filling take? Water has a density of 1000 \(kg/m^3\).
[25] During heavy rain, a section of a mountainside measuring 2.5 km horizontally, 0.80 km up along the slope, and 2.0 m deep slips into a valley in a mud slide.Assume that the mud ends up uniformly distributed over a surface area of the valley measuring \(0.40~ km \times 0.40~ km\) and that mud has a density of 1900 \(kg/m^3\). What is the mass of the mud sitting above a 4.0 m2 area of the valley floor?
[30] Water is poured into a container that has a small leak. The mass m of the water is given as a function of time t by \(m = 5.00t^{0.8} - 3.00t + 20.00\), with \(t \geq 0\), m in grams, and t in seconds. (a) At what time is the water mass greatest, and (b) what is that greatest mass? In kilograms per minute, what is the rate of mass change at (c) t = 2.00 s and (d) t = 5.00 s?