Chapter 8 Potential Energy & Conservation of Energy
Learning Objectives:
In this chapter you will basically learn:
\(\bullet\) Distinguish a conservative force from a nonconservative force.
\(\bullet\) For a particle moving between two points, work done by a conservative force does not depend on which path the particle takes.
\(\bullet\) Calculate the gravitational potential energy of a particle.
\(\bullet\) Calculate the elastic potential energy of a block–spring system.
\(\bullet\) Identify that the mechanical energy of the system is the sum of the kinetic energies and potential energies of those objects.
\(\bullet\) Given a particle’s potential energy as a function of its position x, determine the force on the particle.
\(\bullet\) On a graph of potential energy versus x, superimpose a line for a particle’s mechanical energy and determine the particle’s kinetic energy for any given value of x.
\(\bullet\) On a potential-energy graph, identify any turning points and any regions where the particle is not allowed because of energy requirements.
\(\bullet\) Explain neutral equilibrium, stable equilibrium, and unstable equilibrium.
\(\bullet\) When work is done on a system by an external force with no friction involved, determine the changes in kinetic energy and potential energy.
\(\bullet\) Apply the relationship between average power, the associated energy transfer, and the time interval in which that transfer is made.
8.1 Conservative Forces:
A force is a conservative force if the net work it does on a particle moving around any closed path, from an initial point and then back to that point, is zero. Equivalently, a force is conservative if the net work it does on a particle moving between two points does not depend on the path taken by the particle. The gravitational force and the spring force are conservative forces; the kinetic frictional force is a nonconservative force.
8.2 Work & Potential Energy:
A potential energy is energy that is associated with the configuration of a system in which a conservative force acts. When the conservative force does work W on a particle within the system, the change \(\Delta U\) in the potential energy of the system is
\[\begin{equation} \Delta U = -W. \tag{8.1} \end{equation}\]
If the particle moves from point \(x_i\) to point \(x_f\), the change in the potential energy of the system is
\[\begin{equation} \Delta U = -\int_{x_i}^{x_f} F(x)~dx \tag{8.2} \end{equation}\]
8.3 Gravitational Potential Energy:
Consider a particle of mass m is thrown vertically up along a y axis starting from point \(y_i\) to point \(y_f\), the gravitational force \(\vec F_g\) does work on it. To find the corresponding change in the gravitational potential energy of the particle–Earth system, we use Eq. 8-2 with two changes: (1) We integrate along the y axis instead of the x axis, because the gravitational force acts vertically. (2) We substitute $mg for the force symbol F, because has the magnitude mg and is directed down the y axis. We then have
\[\begin{equation} \Delta U = -\int_{y_i}^{y_f} (-mg)~dy = mg \left [y\right]_{y_i}^{y_f}=mg\left (y_i-y_f\right)=mg\Delta y \tag{8.3} \end{equation}\]
We can assume \(U_i=0\) to be reference gravitational potential energy at a reference point \(y_i\) and the final potential energy \(U_f=U\) of the system at a reference point \(y_f\). Then Eq.8-3 can be rewritten as
\[\begin{equation} U = mgy ~~~(gravitational~potential~energy). \tag{8.4} \end{equation}\]
8.4 Block-Spring Potential Energy:
A block–spring system as shown in Fig. 8-1, with the block moving on the end of a spring of spring constant k. As the block moves from point \(x_i\) to point \(x_f\), the spring force \(F = -kx\) does work on the block.The elastic potential energy of the block–spring system, we substitute kx for F(x) in Eq. 8-2. We then have
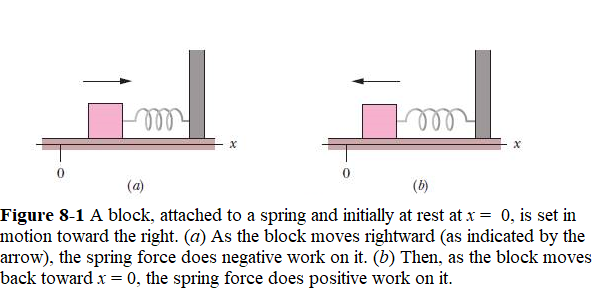
\[\begin{equation} \Delta U = -\int_{x_i}^{x_f} (-kx)~dx = k \left [\frac{x^2}{2}\right]_{x_i}^{x_f}=k\left (\frac{1}{2}x_f^2-\frac{1}{2}x_i^2\right) \tag{8.4} \end{equation}\]
By taking reference potential energy \(U_i = 0\) to be at \(x_i = 0\) and \(U_f = U\) then the elastic potential energy in Eq. 8-4 can be written as
\[\begin{equation} U = \frac{1}{2}kx^2~~~(elastic~potential~energy). \tag{8.5} \end{equation}\]
8.5 Conservation of Mechanical Energy:
8.6 Reading a potential energy curve, work done on a system by an external force, energy due to non-conservative forces, conservation of energy, mass and energy.
(Solved Problems : 2, 6, 17, 23, 31, 34, 38, 39)